model perlemuan element frame dan shell atau solid

Tulisan ini melanjutkan sebelumnya, mengenai pemodelan FE sambungan antara element frame dan shell atau solid yag dihubungkan dengan rigid links.

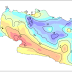
Model SAP untuk Balok kantilever

Hasil analisa,

Defleksi vertikal ujung

Tegangan sumbu utama

Calculation Pads:

' Loads
Pz = 1000 kgf
' Dimension & properties
b = 20cm
h = 20cm
A=b*h= 400.00cm2
Ix = 1/12*b*h^3= 13333.33cm4
K=3/2= 1.50 n.d
Ec=253456.36kg/cm2
G=105606.82kg/cm2
' Section 1
Lx1=100cm
My1 = Pz * Lx1 = 100000.00kgf.cm
y1 = h/2= 10.00cm
y2 = h/4= 5.00cm
fx1 = My1 * y1 / Ix= 75.00kg/cm2
fx2 = My1 * y2 / Ix= 37.50kg/cm2
' FE
fx1s=Avg(80.45,76.92,77.56)= 78.31kg/cm2
fx2s=Avg(41.56,40.145,38.69)= 40.13kg/cm2
' Diff (%)
r1=(1-(fx1/fx1s))*100= 4.23
r2=(1-(fx2/fx2s))*100= 6.56
' Section 2
Lx2=200cm
My2 = Pz * Lx2= 200000.00kgf.cm
fx1 = My2 * y1 / Ix= 150.00kg/cm2
fx2 = My2 * y2 / Ix= 75.00kg/cm2
' FE
fx1s=Avg(151.59,145.74,146.53)= 147.95kg/cm2
fx2s=Avg(76.16,72.70,71.78)= 73.55kg/cm2
' Diff (%)
r1=(1-(fx1/fx1s))*100= -1.38
r2=(1-(fx2/fx2s))*100= -1.98
' Deflection
df=(Pz*Lx2^3)/(3*Ec*Ix)= 0.79cm
ds=(4*K*Ec*Ix)/(A*G*Lx2^2)= 0.01cm
dz=df+ds= 0.80cm
' reffs
dzr = 0.7905= 0.79cm
' Diff (%)
r1=(1-(dz/dzr))*100= -1.34

Beberapa model sederhana diatas ditempuh untuk verified hasil penerapan rigid links penghubung element frame dan element shell atau solid. Pada hubungan element frame dan shell shell biasa digunakan untuk study konsentarasi tegangan daerah titik pertemuan misal balok-kolom baja pengaruh haunched dan stiffener, leleh pada gusset plate pada rangka batang, dll. Pemodelan element shell hanya baik digunakan untuk perilaku lentur dan geser bidang, sedangkan perilaku yang kompleks yaitu torsi dan puntir beserta geometri tidak teratur perlu pengggunaan element solid.

full models

zoomed views

Diatas adalah tahap lanjut pemodelan hubungan element frame dan shell yng diterapkan pada kasus rangka batang guna mempelajari konsentrasi tegangan daerah gusset plate dan besarnya kekangan rotasi ujung batang dimana bisanya pada rangka batang titik buhul diasumsikan sendi. Dalam meredukdi jumlah nodes perlu pemodelan batang double siku hanya dimodelkan tunggal dengan merepkan kondisi simetri.

pandangan dari sisi muka

pembesaran gambar daerah titik buhul (1)

pandangan dari sisi belakang

pembesaran gambar daerah titik buhul (2)

distribusi tegangan leleh kriteria Von-Mises pada gusset plate

pembesaran gambar pada gusset plate

momen pada rangka batang

Pada kasus yang ditinjau saat ini, hasil analisa struktur dgn program bantu SAP menunjukkan adanya 5(lima) titik leleh pada gusset plate. Selain itu juga menunjukan adanya momen sekunder akibat kekangan rotasi titik buhul yang menggunakan sambungan las, dalam kasus ini besarnya adalah sekitar +10% dari tegangan utama/normal (axial), namun disi lain adanya penggunaan faktor panjang effektiff K=1.0 yang lebih besar dari susungguhnya akan memberikan angka aman lebih. Pemodelan diatas juga dapat menghitung faktor panjang efektif sesungguhnya berdasarkan beban kritis/tekuk sumbu utama (in-plane buckling) namun titik buhul yang satu lainnya perlu dimodelkan juga dgn element shell untuk merepresentasikan kekangan rotasi.

**update: meshing masih diterapkan manual, terlihat aspect ratio kurang baik. hasil cara auto quadrilateral terlihat lebih baik.

 

Read More

estimasi tulangan perlu balok beda tinggi

Tulisan ini melanjutkan sebelumnya, mengenai balok tinggi dengan perbedaan dimensi tinggi penampang. Konsentrasi tegangan di sudut patahan pertemuan penampang membuat retakan diagonal, mengenai sudut dan pola retak tergantung dari konfigurasi tulangan yang ditentukan. Program advanded FE yang sudah memasukkan pengaruh nonlinearitas seperti ANSYS/ABAQUS dan ATENA/MERLIN atau lainnya dapat memprediksikan pola retak dan beban ultimit, sedangkan STM hanya pada kapasitas saja dgn nilai batas bawah.

(source: Wang et al, 2005)

Pemodelan STM balok tinggi dgn perbedaan dimensi tinggi, analisa  dan hasil konfigurasi pembesian merujuk pada pustaka El-Metwally et al (2011)





Berikut tampilan model, hasil analis dan perbandingan estimasi kebutuhan tulangan,

Geometri, beban dan kondisi tumpuan

Tegangan prinsipal beton (tebal elemen tidak diperhitungkan penuh)

Alur tegangan utama (warna magenta adalah tekan & warna biru untuk tarik)

Kebutuhan tulangan perlu arah datar (H)

Keutuhan tulangan perlu arah tegak (V)

Grafik perbedaan hasil ditampilkan dgn bar chart berikut,

Terlihat berbeda untuk jenis balok tinggi ini, terutama daerah sudut patahan dimana hasil Elastic FE mendistribusikan pada kedua sisi (atas/bawah, kiri/kanan) sedangkan STM terkonsentrasi salah satu sisi saja. Konsep kedua metode tersebut memang berbeda, sehingga konfigurasi tulangan juga akan berbeda. Perlu pembanding lanjut dengan program nonlinear FE sebagai virtual labs tujuan untuk dasar simulasi model.

calculation pads,

' Ties (T1)
As1a=Avg(12.019,8.585,6.901,6.073,5.246,4.184,3.286,2.352,1.297,0.675)*(2333-1500)*0.9/0.75*2= 10119.55mm2
As1b=Avg(4.911,4.700,4.290,3.685,2.460,1.647,0.833)*(2333-1500)*0.9/0.75*2= 6433.43mm2
' reffs
T1 = 2095kN
Asr = (T1*10^3)/(0.75*460)= 6072.46mm2
Asp = 16*(1/4)*Pi*22^2= 6082.12mm2
' Ties (T2)
As2a=Avg(9.458,6.829,4.283,3.667,2.655,2.259,1.768,1.414,1.107,0.777,0.923,0.604,0.468)*(6250-5615)*0.9/0.75*2= 4245.16mm2
As2b=Avg(9.458,5.706,1.955,0.384,0.337,0.190,0.086)*(6693-6250)*0.9/0.75*2= 2751.56mm2
' reffs
T2 = 1091kN
Asr = (T2*10^3)/(0.75*460)= 3162.32mm2
Asp = 2*14*(1/4)*Pi*12^2= 3166.73mm2
' Ties (T3)
As1a=Avg(1.067,3.165,2.488,1.599,1.518,1.436,1.144,0.851)*(750-0)*0.9/0.75*2= 2985.30mm2
As1b=Avg(1.516,1.439,1.380,1.322,1.265,1.160,1.055,0.975,0.896)*(750-0)*0.9/0.75*2= 2201.60mm2
As1c=Avg(12.019,7.343,0.4289,0.314,0.200,0.139,0.0786,0.0628,0.047)*(1500-750)*0.9/0.75*2= 4126.46mm2
' reffs
T3 = 1091kN
Asr = (T3*10^3)/(0.75*460)= 3162.32mm2
Asp = 10*(1/4)*Pi*20^2= 3141.59mm2

Read More

melihat rujukan kuat geser balok beton tanpa begel

Parameter yang mempengaruhi kuat geser balok beton tanpa begel diantaranya adalah dimensi:lebar & tinggi effektif, mutu beton (f'c),  perbandingan jarak titik geser terhadap tinggi effektif, perbandingan nilai geser ultimit (Vu) dan momen ultimit (Mu).
[scribd id=63218770 key=key-2ne6x387evayattdn8n mode=list]

Berikut plot grafik bar chart kuat geser balok tanpa begel dari beberapa rujukan,



Selanjutnya dilakukan perbandingan dgn program analisa penampang beton dengan model tanpa begel dan dipasang begel minimum. Terlihat hasilnya yaitu (90.7kN dan 102.8kN) sedikit lebih kecil atau mendekati dibandingkan kebanyakan rujukan.

Dimensi, mutu baja & beton serta tulangan terpasang.

Balok beton tanpa begel

Balok beton dgn begel dibawah minimum

Read More

estimasi tulangan perlu balok tinggi jenis corbel

Tulisan ini melanjutkan sebelumnya, mengenai balok tinggi jenis corbel. Rujukan pustaka dari Singh etal (2005), pembebanan dan geometri simetris sehingga hanya dimodelkan separuh untuk mereduksi DOF's dan waktu penyelesaian.

Loads, Geometry and STM models (source: Singh etal, 2005)

Elastic Linear FE models & results



 

fig.2



fig.3



 

 

fig.4

Reinforce bars arrangement

(source: Singh etal, 2005)

Kontur kebutuhan tulangan perlu hasil SAP

Arah datar (H)

Arah Tegak (V)

Calculation pads,

' Horizontal
As1=Avg(8.661,3.861,2.449,1.464,1.158)*(750-627)*0.9/0.75*2 = 1038.69 mm2
' Reffs
Asr = (284.68*10^3)/(0.75*415) = 914.63 mm2
Asp = 6*0.25*Pi*16^2 = 1206.37 mm2
' Vertical
As2=Avg(1.307,1.296,0.656,1.259,0.527)*(300-250)*0.9/0.75*2 = 121.08mm2
' Reffs
Asmin=283.3 mm2

Read More

estimasi tulangan perlu balok tinggi berlubang

Tulisan ini melanjutkan sebelumnya, mengenai hasil pembesian tulangan balok tinggi dengan elastic FE program bantu SAP. Keadaan lain yang ditinjau adalah pengaruh adanya lubang.

Elastic FE models

Stress path

Concrete principal stress

Elastic Linear FE

Nonlinear FE (Muttoni etal, 2007)

STM models

(source: Muttoni etal, 2007)

fig.3

(source: Steven etal, 2000)

Reinforce bars arrangement

fig.4

fig.5

Kontur tulangan perlu arah datar (H)

Kontur tulangan perlu arah tegak (V)

Perbedaan hasil ditampilkan dengan bar chart berikut,



Pola retak dan kapasitas beban ultimit pada beberapa jenis model STM dan konfigurasi tulangan hasil penelitian Maxwell, B.S. (1996) dgn scaled down 5.5



Terlihat konfigurasi tulangan orthogonal dgn kombinasi diagonal menghasilkan kapasitas beban ultimit lebih besar dibandingkan konfigurasi tulangan lainnya. Semua model mencapai beban terfaktor yg direncanakan sebesar 22Kips (Maxwell, 1996)

 

calculation pads,

' Horizontal bars Reinforcement
As1=Avg(3.599,1.735,0.719,0,0)*500*0.9/0.75= 726.36
reff1a=2*0.25*Pi*25^2= 981.75
reff1b=2*0.25*Pi*20^2= 628.32
As2=Avg(2.558,0.702,1.267,1.124,0.878)*500*0.9/0.75= 783.48
reff2a=2*0.25*Pi*25^2= 981.75
reff2b=3*0.25*Pi*20^2= 942.48
As3=Avg(3.833,2.095,1.359)*(2338-2000)*0.9/0.75= 985.20
reff3a=2*0.25*Pi*25^2= 981.75
As3=Avg(3.833,2.095,1.359,0.698)*(2675-2000)*0.9/0.75= 1616.96
reff3b=7*0.25*Pi*16^2= 1407.43
As4=Avg(2.775,0.0386,0.0481,0.031,0.005,0.073,0)*(2000-500)*0.9/0.75= 763.89
reff4=6*0.25*Pi*12^2= 678.58
As5=Avg(3.832,0.553,0.153,0.102,0,0.143,0)*(2000-500)*0.9/0.75= 1229.91
reff5=6*0.25*Pi*12^2= 678.58
' Vertical bars Reinforcement
As1=Avg(3.343,1.716,1.165,0.700)*(2625-2000)*0.9/0.75= 1298.25
reff1a=2*0.25*Pi*25^2+2*0.25*Pi*12^2= 1207.94
As1=Avg(3.343,1.716,1.165,0.700,0.456)*(2938-2000)*0.9/0.75= 1661.39
reff1b=7*0.25*Pi*16^2= 1407.43
As2=Avg(0,0.640,0.097,0.153,0.148,0.571,3.343)*(2000-500)*0.9/0.75= 1273.37
reff2a=7*0.25*Pi*12^2= 791.68
reff2b=6*0.25*Pi*12^2= 678.58
As3=Avg(0.049,0.021,0.027,0.025,0.029,0.027,0.027,0.0258,0.027,0.022,0.029,0.018,0.04,0.027,0.06,0.071,0.121,0.258,0.492,2.6180)*(7000-2000)*0.9/0.75= 1204.14
reff3a=16*0.25*Pi*12^2= 1809.56
reff3b= 0.00
' Minimum bars reinforcement
A_smin=0.002*1000*400-50= 750.00

Read More

kontribusi kekakuan balok sekunder

Tulisan ini merupakan kelanjutan dari sebelumnya, mengenai distribusi beban dua arah pada struktur beton bertulang dimana saat ini ditinjau pengaruh balok sekunder/pembagi yang biasa ditemui pada bangunan lokal.

The actual distribution of loads on these elements is quite complex. ETABS uses the concept of tributary loads as a simplifying assumption for transforming the loads (CSi,1999)

I took simple frame models to check, it contains secondary beams with different stiffness near to 4 times lower compared to main beams.



Figures above shows extruded 3d views, left models with automatic area loads to frame done by SAP another using finite element models with considering beam to slab eccentricity.



Bending moment diagrams, right models has low values.



Zero axial force in beams for left models, contrary high axial force (tension) exist in right models due to eccentricity modeling with rigid links.



Slab act in compression by couple tension force in beams, it may be figuring as tee-beam with flanges effective width.

(source: Chiewanichakorn, etal. 2001)

Using tributary areas load concept will ignore variable stiffness of beams  in a panel being considered. FE models do betters in prediction but required  additional nodes and computational effort. In case slab panel  with secondary beams, bending moment will varies depending geometry and beams sectional properties. Another approach is remove secondary beams with equivalent slab stiffness with modified flexural rigidities of plates may required for this cases to avoid unacceptable results and it's behavior.

Calculation pads,

' Tributary area concept
' Beam-Y
' B30/60
M_1 = 69.7;
' B30/40
M_2 = 69.56;
' Beam-X
' B30/60
M =116.49;
' FE approximation
' Beam-Y
' B30/60
M_e=40.59
M_a=177.06*0.24= 42.49
M=M_e+M_a= 83.08 kN.m
' B30/40
M_e=32.32
M_a=168.63*0.14= 23.61
M=M_e+M_a= 55.93 kN.m
' Beam-X
' B30/60
M_e=67.93
M_a=214.46*0.24 = 51.47
M=M_e+M_a = 119.40 kN.m
' Flexural Reinforcement (hand calculations)
' Tributary approximation
' Beam-Y
' A_s1 < A_smin = 590.10 mm2 (B30/60)
' A_s2 = 634.89 mm2 (B30/40)
' Beam-X
' A_s = 672.62 mm2
' FE approximation
' Beam-Y
' A_s1 < A_smin = 590.10 mm2 (B30/60)
' A_s2 = 502.10 mm2 (B30/40)
' Beam-X
' A_s = 690.11 mm2 (B30/60)
'
' Beam Stiffness Ratio (middle & edge)
E_c=(4700*Sqrt(25))*10.19716= 239633.26 kgf/cm2
L = 600 cm
b1 = 30 cm
h1 = 60 cm
Ix1=1/12*b1*h1^3= 540000.00 cm4
b2 = 30 cm
h2 = 40 cm
Ix2=1/12*b2*h2^3= 160000.00 cm4
K_db1 = (48*E_c*Ix1)/L= 10352156832.00
K_db2 = (48*E_c*Ix2)/L= 3067305728.00
R_db=K_db1/K_db2= 3.38 (~4 times stiffness)
' Beam internal moment ratio (secondary beams 30/40)
M_x1 = 69.56;
M_x2 = 55.93;
R_mx = M_x1/M_x2= 1.24 (~ 25%higher)

' Beam internal moment ratio (main beams 30/60)

M_x3 = 69.70;
M_x4 = 83.08;
R_mx = M_x3/M_x4= 0.84 (~15%lower)

Read More