dominasi geser pd web balok baja berlubang

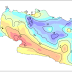
Ditinjau distribusi tegangan balok baja berlubang (castellated) WF300 + adding plates dgn tinggi balok jadi 60cm dan bentang 6,1m...Distribusi tegangan S11 (searah X-global). Distribusi tegangan S22 (searah Z-global). Lendutan arah-z pd tengah bentang, dz ~ 6.5mmDari prediksi perhitungan dibawah menunjukkan bahwa dominasi geser akibat aksi vierendeel...

Read More

masalah kontak sederhana suatu balok

masalah kontak sederhana (tanpa gesekan) dapat dianalisa dgn program bantu SAP2000, berikut ditinjau balok kantilever (kanan) yang menerima beban terpusat P. Akibat beban tersebut terjadi defleksi sebesar ~3.5cm, apabila jarak serat tepi bawah balok kanan dgn serat tepi atas balok kiri ada gap lebih kecil dari nilai diatas, maka balok kiri tersebut...

Read More