material beton dengan MFront dalam CalculiX

sebelumnya telah ditinjau mengenai material tanah pada CalculiX (Mohr-Coulomb(Hardening)) dan juga TFEL/MFront (MohrCoulombAbboSloan) maka selanjutnya ditinjau untuk material beton. Adapun contoh yg diambil adalah beberapa model yg telah diuji dan diteliti sebelumnya yg berbentuk polos, dengan coakan dan adanya tulangan. Perhitungan modulu elastisitas, kuat tarik dan fracture energy pada dapat mengacu penelitian dan peraturan seperti CEB-FIP 1990 namun telah diberikan. Perlu dilakukan perhitungan ulang dengan pendekatan rumusan (back calculation), karena hubungannya dengan paramater kuat tarik dan fracture energy yg sudah terukur.  Perhitungan parameter tersebut dipengaruhi oleh diamater agregat kasar, rasio air semen dan bentuk agregat apakah mendekati bulat atau tajam bersudut persegi. 

.

.

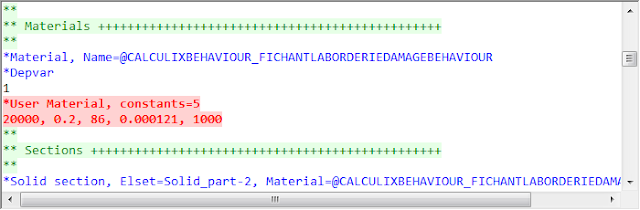
jika CalculiX dikombinasikan dengan library material MFront pastinya akan sangat lengkap, solver internal saja sudah mempunyai jenis CompresionOnly dan Mohr-Coulomb(Hardening) untuk beton, sedangkan pada MFront ada beberapa yaitu: MohrCoulombAbboSloan, DruckerPrager, DruckerPragerCap, Marigo, Mazars, UnilateralMazars dan FichantLaBorderie. Dua jenis yg terakhir dapat untuk beban siklis dengan adanya riwayat menjadikan kondisi retak terbuka dan tertutup kembali. Rujukan yg sya gunakan adalah paper dari Arruda et al (2021) dan Grassl et al (2013) juga Martínez et al (2014) sedangkan material yg digunakan adalah semua jenis tersebut pada kasus pertama, kasus lainnya lebih fokus pada material model dari Mazars dan FichantLaBorderie karena pertimbangan kelebihan tadi. Pemodelan yg sya buat mungkin agak sedikit berbeda pada beban terpusat yg sya jadikan bebam permukaan selebar tertentu (neglibible) hanya untuk menghindari singularitas pada solver CalculiX. 

.

.

.

.

Model material CompressionOnly (CalculiX Umat) hasilny cukup memberikan gambaran awal yaitu: tegangan tarik prinsipal hanya pada 2.25MPa pada beban titik sebesar 7500N, regangan tarik prinsipal absolut sebesar 0.01 yang sudah melebihi batas maksimum beton yg umumnya berkisar 0.00015~0.0002, sedangkan regangan tekan maksimum masih kecil yaitu sebesar 0.0002 masih dibawah umumnya beton yg berkisar 0.003~0.0035 yg artinya belum terjadi kerusakan akibat tekan (crushing). Hasil plot beban dan defleksi keatas menunjukan sebesar 0/35mm yg lebih kecil dari maksimum yg terjadi sesungguhnya, dua atau tiga kali nilai ini dapat digunakan sebagai beban defleksi untuk mengetahui tahapan kerusakan (damage evolution) pada model yg ditinjau. 

.

.

.

.

.

.

Model material Mohr-Coulomb (CalculiX internal) hasilnya pada tegangan tarik prinsipal pada 3.59MPa pada beban titik sebesar 7500N, regangan tarik prinsipal absolut sebesar 0.00021 dan regangan plastis ekivalen hanya sebesar 0.000073 (?) yang dapat saja sudah melebihi batas maksimum beton yg umumnya berkisar 0.00015~0.0002, sedangkan regangan tekan maksimum masih kecil yaitu sebesar 0.00011 masih dibawah umumnya beton yg berkisar 0.003~0.0035. Hasil plot beban dan defleksi keatas menunjukan sebesar 0.13mm yg jauh lebih kecil dari maksimum yg terjadi sesungguhnya

.

.

.

.

.

.

.

Model material MohrCoulombAbboSloan (TFEL MFront) hasilnya pada tegangan tarik prinsipal sebesar 3.09MPa pada beban titik sebesar 7500N, regangan tarik prinsipal absolut sebesar 0.0028 dan regangan plastis ekivalen sebesar 0.0016 yang kemungkinan sudah melebihi batas maksimum beton yg umumnya berkisar 0.00015~0.0002, sedangkan regangan tekan maksimum masih kecil yaitu sebesar 0.0011 masih dibawah umumnya beton yg berkisar 0.003~0.0035. Hasil plot beban dan defleksi keatas menunjukan sebesar 0.136mm yg lebih kecil dari maksimum yg terjadi sesungguhnya

.

.

.

.

.

.

.

.

Model material DruckerPrager (TFEL MFront) hasilnya pada tegangan tarik prinsipal sebesar 4.97MPa pada beban titik sebesar 7500N, regangan tarik prinsipal absolut sebesar 0.0018 yang kemungkinan sudah melebihi batas maksimum beton yg umumnya berkisar 0.00015~0.0002, sedangkan regangan tekan maksimum masih kecil yaitu sebesar 0.00012 masih jauh dibawah umumnya beton yg berkisar 0.003~0.0035. Hasil plot beban dan defleksi keatas menunjukan sebesar 0.127mm yg lebih kecil dari maksimum yg terjadi sesungguhnya

.

.

.

.

.

.

Model material DruckerPragerCap (TFEL MFront) hasilnya pada tegangan tarik prinsipal sebesar 4.96MPa pada beban titik sebesar 7500N, regangan tarik prinsipal absolut sebesar 0.0028 yang kemungkinan sudah melebihi batas maksimum beton yg umumnya berkisar 0.00015~0.0002, sedangkan regangan tekan maksimum masih kecil yaitu sebesar 0.00011 masih jauh dibawah umumnya beton yg berkisar 0.003~0.0035. Hasil plot beban dan defleksi keatas menunjukan sebesar 0.127mm yg lebih kecil dari maksimum yg terjadi sesungguhnya

.

.

.

.

.

.

Model material Mazars (TFEL MFront) tidak dapat mencapai konvergensi pada beban permukaan sebesar 7500N.

.

.

.

.

.

.

.

.

digunakan beban defleksi sebesar 0.3mm dan dilakukan penghalusan mesh sebesara satu setengah kalinya. Solver belum mencapai konvergensi dan hasil ditunjukan dengan hubungan tahap defleksi dan reaksi perletakan, hanya mencapai sekitar 3600N.

.

.

.

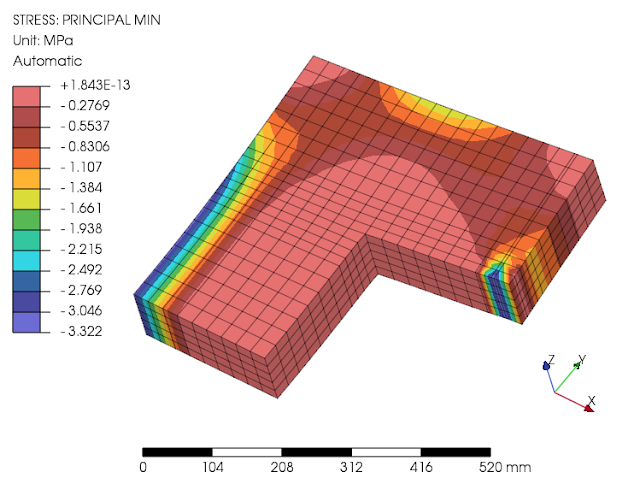
Model material FichantLaBorderie (TFEL MFront) dapat mencapai konvergensi pada beban permukaan sebesar 7500N.

.

.

.

.

.

.

.

ditetapkan beban defleksi sebesar 0.6mm terlihat model material damage dari FichantLaBorderie lebih stabil dan cepat mencapai konvergensi dibandingkan sebelumnya. Perlu mempelajari lebih lanjut pengaruh ukuran mesh terhadap nilai parameter lain. Hasil grafik agak sedikit berbeda, nilai puncak gaya reaksi terbesar (7687N) berada pada posisi beban defleksi sebesar 0.153mm, namun ini sudah cukup memberikan gambaran jarena beban maksimum yg diterima sudah hampir sama dengan hasil penelitian sebelumnya.

.

.

.

.

.

saat dilakukan perbaikan model dengan mesh yg lebih rapat maka faktor Bt perlu disesuaikan dengan ukuran mesh yg digunakan menjadi 443 agar hasilnya dapat sesuai bertahan, jika tidak dilakukan akan menunjukan lebih kecil dari sebelumnya. 

.

.

.

terlihat juga hasil lebih tinggi pada nilai damage scale dibandingkan sebelumnya, kemungkinan semakin rapat nilainya akan mendekati 1.0 yg menunjukkan konvergensi. Keterbatasan model ini adalah nilai parameter yg perlu menyesuaikan mesh yg digunakan sehingga diperlukan mesh yg merata uniform pada daerah retak seperti beban terpusat atau tumpuan, namun untuk lebih mudahnya dibuat mendekati sama untuk keseluruhan bagian.

.

.

.

.

.

.

.

jenis material yg digunakan adalah model plastis DruckerPragerCap dan damage FichantLaBorderie dari libraray MFront, hasilnya ditampilkan berikut.

.

.

.

.

.

.

.

.

.

.

.

.

saat menggunakan beban adalah gaya solver CalculiX tidak dapat mencapai konvergensi, untuk itu dibuat beban adalah defleksi sebsar 1.0mm arah vertikal kebwaha (negatif) yntuk mengetahui gaya rekasi u;timit yg dapat ditahan. Hasilnya menunjukan lebih kecil dari uji experiemental yaitu sebesar 885N pada beban defleksi 0.125mm dan ini perlu dicari penyebanya y mungkin dari tingkat kerapatan mesh daerah terdekat.

.

.

.

perbaikan model dengan penghalusan mesh daerah jalur retakan, nilai Bt perlu diubah menyesuaikan yaitu senilai 60, hasilnya terlihat menunjukan peningkatan mendekati beban ultimit hasil uji expereimental, nilai damage index juga menjadi 1.0 dan kelihtannya model ini perlu mesh yg sangat halus.

.

.

.

.

pada makalah rujukan kurang jelas mengenai ketebalan keluar bidang gambar, kelihatannya diasumsikan sebagai elemen plane-strain dengan asumsi yg biasanya diambil 1.0m atau 1000mm maka untuk ketebalan 200mm yg sya gunakan pada model solid tiga dimensi dipakai beban sebesar 60kN.  Namun setelah dilakukan analisa material plastis dengan CalculiX hasilnya menunjukkan terlalu rendah, penggunaan material damage yaitu pada beban sebesar 240kN

.

.

.

.

.

.

.

.

.

.

.

.

dilakukan perbaikan model dengan penghalusan mesh, ditentukan beban adalah defleksi sebesar 0.35mm menunjukan hasil gaya reaksi maksimum sekitar 256kN yg masih dibawah hasil uji eksperimental yg dapat mencapai 350kN, Kelihatannya memang analisa jenis ini membutuhkan tingkatan mesh yg sangat halus untuk mencapai konvergensi sesuai aktualnya.

.

.

.

.

.

.

.

.

.

.

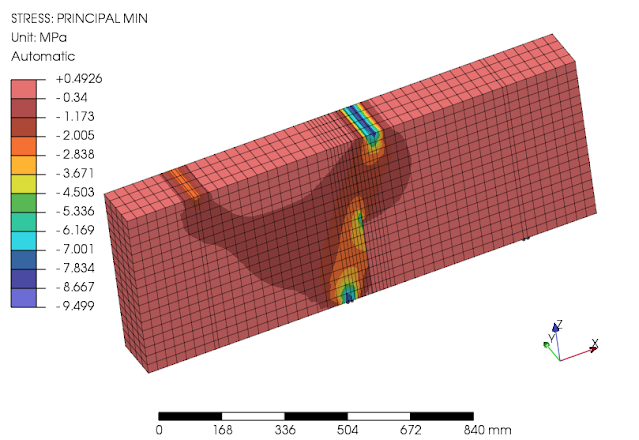
model dengan adanya notch yg tipis mendekati ketebalan nol dalam hal ini dipakai sebesar 2mm cukup sulit mencapai konvergensi namun sudah baik (~125kN) dapat mencapai beban mendekati yg diterapkan. Kelihatannya perlu mesh yg sangat halus untuk model ini dan perlu peninjauan lanjut dengan perbaikan.

.

.

.

.

.

.

.

dilakukan perbaikan mesh dengan penghalusan daerah retakan, nilai damage scale meningkat pda beban sebesar 124kN total reaksi tumpuan masih lebih kecil dari yg diterapkan.

.

.

.

.

.

.

..

.

.

.

.

.

.

.

.

.

.

.

.

.

.

Read More