Kamis, 09 Oktober 2008
Minggu, 21 September 2008
Perbandingan RC Shell reinforcement design pd slab&beam
Dilihat perbandingan hasil design slab beton berdasarkan force method (SAFE) dan moment resultant atau predetermined field moment (SAFE/SAP2000), slab tersebut sudah ditinjau dan dianalisa sebelumnya.
Data perhitungan :
Tebal slab, th = 150 mm
Selimut beton,
Tulangan atas (Top)
X cover = 20 mm (to centroid)
Y cover = 30 mm
Tulangan bawah (Bottom)
X cover = 20 mm (to centroid)
Y cover = 30 mm
Mutu beton, f'c = 27.5 MPa
Baja, fy = 400 MPa (deformed bars)
Faktor reduksi kekuatan tinjauan lentur, Phi_b = 0.9 (ACI318 dan default SAP2000)
Kombinasi yg ditinjau U=1.4D+1.7L

Design method using Nodal Moment (force method)
Hasil desain SAFE
Middle Strip
Lapangan
As_pos = 1104.11 mm2/m lebar strip
Tumpuan
As_neg = 801.36 mm2/m lebar strip

Hasil Design SAP2000
Lapangan
As_pos = Avg(0.590746,0.676456,0.676456,0.590746) = 0.633601 mm2/mm'
= 0.633601*3000 = 1900.80 mm2/m lebar strip
Tumpuan
As_neg = Avg(0.275341,0.286297,0.286297,0.275341) = 0.280819 mm2/mm'
= 0.280819*3000 = 842.457 mm2/m lebar strip
Perbedaan yang cukup signifikan terutama pada pembesian momen positif (lapangan). Pada desain beton slab/plate (XY plane,without membrane forces) didasarkan hubungan kesetimbangan (Tension steel) Ts = Cc (Conpression concrete), ini terlihat berbeda pada desain shell (3D,with membrane forces) SAP2000 yang didasarkan pada konversi bending moment thd lengan momen yg menjadikan pure membrane forces ditambahkan dengan membrane forces yg terjadi. Tidak diberikan dan dijelaskan dalam dokumentasi SAP2000 - shell reinforcement mengenai batasan validitas penggunaan, apakah dapat juga diterapkan pada element plate (bending only) atau element plane stress (membrane only), perlu merujuk pada pustaka aslinya dari Troels-Brondum-Nilsen(1974) dan Peter Marti (1990) untuk mengetahui detail dan kejelasannya.
Sebagai peninjauan awal saja, ditinjau aplikasi desain element shell SAP2000 untuk keadaan membrane force only yaitu struktur balok yang dimodelkan dgn element plane stress
Data perhitungan :
Lspans = 6.00m
Dimensi balok, BxH = 400x1000 mm
Mutu beton K300 --> f'c = 25.38 MPa
Tulangan fy = 400 MPa (deformed bars)
Tebal shell, th = 400 mm
Beban P = 2.22*6 = 13.33 kN
Momen Mu = 13.33*6.00 = 80.0 kN.m
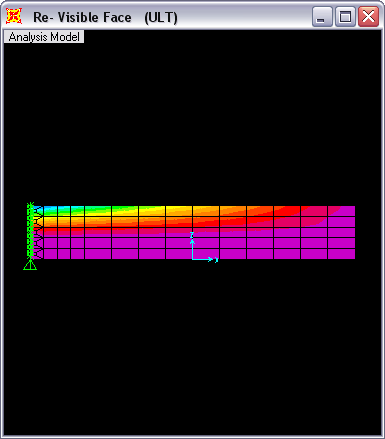
Perhitungan standar desain balok beton ACI-318 dengan faktor Phi_b = 0.9 dapat dilihat disini, perkiraan kebutuhan kebutuhan tulangan perlu berkisar 4D10 (314.16mm2) tergantung konfigurasi tulangan.
Hasil output kebutuhan penulangan daerah tumpuan (negatif moment)
Nilai terbesar @h=1000mm, As_req(max) =
Max(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.66032 = mm2/mm'
Nilai rata-rata, As_req(avg) =
Avg(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.327452889 mm2/mm'
As_req = 0.327452889*(1000-466.67)*2 = 349.28 mm2
Nilai terkecil@h=466.67mm, As_req(min) = Min(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.012451 mm2/mm'

Jika ditinjau penulangan per-lapis
Lapis atas Hlap1 = 200 mm @ h=800~1000mm
Tinjau rata-rata, As_req(avg)=Avg(0.66032,0.595727,0.474602,0.405285,0.337724)
= 0.5339835 mm2/mm'
As_req(lap1) = 0.5339835*200*2 = 213.59 mm2
Lapis atas Hlap2 = 200 mm @ h=600~800mm
Tinjau rata-rata, As_req(avg)=Avg(0.66032,0.595727,0.474602,0.405285)
= 0.2805375 mm2/mm'
As_req(lap2) = 0.2805375*200*2 = 112.22 mm2
Lapis atas Hlap3 = 200 mm @ h=400~600mm
Tinjau rata-rata, As_req(avg)=Avg(0.157382,0.081826,0.012451,0.00)
= 0.06291475 mm2/mm'
As_req(lap3) = 0.06291475*200*2 = 25.17 mm2
Jumlah total, As_req(tot)= 213.59+112.22+25.17 = 350.98 mm2
Terlihat nilainya mendekati dibandingkan dengan perhitungan balok beton biasa (349.28mm2 atau 350.98mm2 terhadap 314.16mm2), namun perlu tambahan perbandingan lain seperti balok tinggi (deep) atau miring (haunched). Beberapa rujukan menyatakan bahwa perhitungan design moment pada element shell dgn menggunakan moment resultant (wood-armer) atau predetermined field moment sangat sensitif terhadap meshing yang digunakan (required fine mesh). Perlu adanya penulurusan verifikasi/validasi dari rujukan pustaka aslinya, sehingga didapat lebih kejelasan.
Data perhitungan :
Tebal slab, th = 150 mm
Selimut beton,
Tulangan atas (Top)
X cover = 20 mm (to centroid)
Y cover = 30 mm
Tulangan bawah (Bottom)
X cover = 20 mm (to centroid)
Y cover = 30 mm
Mutu beton, f'c = 27.5 MPa
Baja, fy = 400 MPa (deformed bars)
Faktor reduksi kekuatan tinjauan lentur, Phi_b = 0.9 (ACI318 dan default SAP2000)
Kombinasi yg ditinjau U=1.4D+1.7L

Design method using Nodal Moment (force method)
Hasil desain SAFE
Middle Strip
Lapangan
As_pos = 1104.11 mm2/m lebar strip
Tumpuan
As_neg = 801.36 mm2/m lebar strip

Hasil Design SAP2000
Lapangan
As_pos = Avg(0.590746,0.676456,0.676456,0.590746) = 0.633601 mm2/mm'
= 0.633601*3000 = 1900.80 mm2/m lebar strip
Tumpuan
As_neg = Avg(0.275341,0.286297,0.286297,0.275341) = 0.280819 mm2/mm'
= 0.280819*3000 = 842.457 mm2/m lebar strip
Design method using predetermined field moment (SAP2000 RC Shell Design)
Perbedaan yang cukup signifikan terutama pada pembesian momen positif (lapangan). Pada desain beton slab/plate (XY plane,without membrane forces) didasarkan hubungan kesetimbangan (Tension steel) Ts = Cc (Conpression concrete), ini terlihat berbeda pada desain shell (3D,with membrane forces) SAP2000 yang didasarkan pada konversi bending moment thd lengan momen yg menjadikan pure membrane forces ditambahkan dengan membrane forces yg terjadi. Tidak diberikan dan dijelaskan dalam dokumentasi SAP2000 - shell reinforcement mengenai batasan validitas penggunaan, apakah dapat juga diterapkan pada element plate (bending only) atau element plane stress (membrane only), perlu merujuk pada pustaka aslinya dari Troels-Brondum-Nilsen(1974) dan Peter Marti (1990) untuk mengetahui detail dan kejelasannya.
Sebagai peninjauan awal saja, ditinjau aplikasi desain element shell SAP2000 untuk keadaan membrane force only yaitu struktur balok yang dimodelkan dgn element plane stress
Data perhitungan :
Lspans = 6.00m
Dimensi balok, BxH = 400x1000 mm
Mutu beton K300 --> f'c = 25.38 MPa
Tulangan fy = 400 MPa (deformed bars)
Tebal shell, th = 400 mm
Beban P = 2.22*6 = 13.33 kN
Momen Mu = 13.33*6.00 = 80.0 kN.m

Perhitungan standar desain balok beton ACI-318 dengan faktor Phi_b = 0.9 dapat dilihat disini, perkiraan kebutuhan kebutuhan tulangan perlu berkisar 4D10 (314.16mm2) tergantung konfigurasi tulangan.
Hasil output kebutuhan penulangan daerah tumpuan (negatif moment)
Nilai terbesar @h=1000mm, As_req(max) =
Max(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.66032 = mm2/mm'
Nilai rata-rata, As_req(avg) =
Avg(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.327452889 mm2/mm'
As_req = 0.327452889*(1000-466.67)*2 = 349.28 mm2
Nilai terkecil@h=466.67mm, As_req(min) = Min(0.66032,0.595727,0.474602,0.405285,0.337724,0.221759,0.157382,0.081826,0.012451)
= 0.012451 mm2/mm'

Jika ditinjau penulangan per-lapis
Lapis atas Hlap1 = 200 mm @ h=800~1000mm
Tinjau rata-rata, As_req(avg)=Avg(0.66032,0.595727,0.474602,0.405285,0.337724)
= 0.5339835 mm2/mm'
As_req(lap1) = 0.5339835*200*2 = 213.59 mm2
Lapis atas Hlap2 = 200 mm @ h=600~800mm
Tinjau rata-rata, As_req(avg)=Avg(0.66032,0.595727,0.474602,0.405285)
= 0.2805375 mm2/mm'
As_req(lap2) = 0.2805375*200*2 = 112.22 mm2
Lapis atas Hlap3 = 200 mm @ h=400~600mm
Tinjau rata-rata, As_req(avg)=Avg(0.157382,0.081826,0.012451,0.00)
= 0.06291475 mm2/mm'
As_req(lap3) = 0.06291475*200*2 = 25.17 mm2
Jumlah total, As_req(tot)= 213.59+112.22+25.17 = 350.98 mm2
Terlihat nilainya mendekati dibandingkan dengan perhitungan balok beton biasa (349.28mm2 atau 350.98mm2 terhadap 314.16mm2), namun perlu tambahan perbandingan lain seperti balok tinggi (deep) atau miring (haunched). Beberapa rujukan menyatakan bahwa perhitungan design moment pada element shell dgn menggunakan moment resultant (wood-armer) atau predetermined field moment sangat sensitif terhadap meshing yang digunakan (required fine mesh). Perlu adanya penulurusan verifikasi/validasi dari rujukan pustaka aslinya, sehingga didapat lebih kejelasan.
Selasa, 16 September 2008
Distribusi beban lantai ke balok: Auto,Trapezoidal,Equivalen

Dalam pendistribusian beban lantai untuk jenis struktur beton yang dicor bersamaan/monolit maka kebanyakan distribusi beban yang bekerja adalah pada dua arah (two-ways). Setiap program analisa struktur mempunyai berbagai pilihan untuk memperhitungkan beban yg bekerja pada balok, pada SAP2000 versi 10 keatas sudah tersedianya kemampuan pemberian input beban secara auto aksi satu arah (one-way) atau dua-arah(two-ways) tergantung penentuan oleh pengguna. Beban merata yang bekerja (force/square length) akan didistribusaikan ke balok yang bertemu menjadikan beban (force/length) trapesium dan segitiga. Ditinjau balok penumpu beban lantai tanpa adanya balok rib atau balok anak/sekunder, dengan data perhitungan :
Beban merata
W = 10.00 kN/m2
Berat sendiri balok tidak ditinjau terlebih dahulu untuk kejelasan penyampaian.
Bentang
Lx = 4.00m (Shortest spans)
Ly = 6.00m (Longest spans)
Perbandingan Ly/Lx = 6.00/4.00 = 1.5 < 2.5 maka distribusi beban dua arah.

Adapun pemodelan yang ditinjau adalah
Model 1, beban di-inputkan sebagai beban merata (W arah -Z) ditentukan two-ways.
Model 2, beban dikerjakan langsung pada balok. Pada nilai terbesar (peak values)
qTrap = qSgt = (1/2)* W * Lx = 0.5*10.00*4.00 = 20.00 kN/m'
Model 3, beban trapesium dan segitiga dijadikan merata sepanjang balok dengan equivalensi didasarkan kondisi tumpuan sederhana.
qEqvTrap = 0.5 * W * Lx *((Ly^2-(4/3)*(Lx/2)^2)/Ly^2) = 17.04 kN/m'
qEqvSgt = (W * Lx)/3 = 13.33 kN/m'

Pertama ditinjau tumpuan sederhana hinged, kemudian ditinjau ulang pada keadaan tumpuan lain/kombinasi: rolled, free, fixed dan kolom bawah jepit (b=h=30cm;Lkol=3.0m).

Tinjauan tumpuan fixed-free @shortest(selisih 22.84%)

Tinjauan tumpuan fixed-hinged-free (selisih 21.34%)

Tinjauan tumpuan fixed-free (selisih 25.16%)

Tinjauan tumpuan kolom @ satu bentang (selisih 3.76%)


Tinjauan tumpuan kolom @ dua bentang (selisih 4.40%)

Tinjauan tumpuan kolom @ dua bentang + kantilever (selisih 19.44%)
Distribusi beban aksi dua arah yg auto pada SAP2000 terlihat stabil, namun bagaimana dgn aksi satu-arah hubungannya dgn penentuan sisi yg menjadi tumpuan (shortest by default?) jika berupa lembaran papan kayu/beton yg panjang atau keadaan lain bondeck dipasang sejajar arah memanjang (fungsi ruang sebelah,cost,bentang selisih sedikit) bagaimana? default's not always be the best, i think :)
Pada tinjauan balok dgn tumpuan diatas, selisih mencapai ~25% sedangkan pada portal tidak bertingkat kondisi umum sperti diatas selisih kurang dari 5% (dapat diterima). Selisih akan besar pada portal yg terdapat kantilever. Kelanjutan tinjau terhadap adanya dinding beton dan portal bertingkat.
Kamis, 11 September 2008
Momen Rencana (Pelat) dengan mengekstrak hasil element 2D Shell

Penggunaan element 2D/3D shell perlu digunakan dalam desain struktural seperti pelat lantai dan dinding penahan tanah. Menurut beberapa rujukan desain element pelat beton bertulang dengan FE element shell dikenal dua metode yaitu force method dan resultant method atau lebih dekenal metode wood-armer , perbedaannya yg terakhir memperhitungkan twisting pelat (Mxy) sedangkan pada force method tidak namun memenuhi equilibrium. Beberapa rujukan juga menyatakan pada keadaan umum force method sudah mencukupi, namun pada keadaan khusus pelat yg mengalami torsi besar seperti akibat ketidak simetrisan tepi penumpunya atau adanya beban/tumpuan terpusat sembarang. Indikasi tidak memenuhi penggunaan force method dapat diperkirakan dari perbandingan nilai torsi pelat Mxy terhadap Mx atau My yg lebih besar dari 0,10. Metode moment resultant tersebut direkomendasikan oleh Park&Gamble.

**SAFE (BeamBot,Top,Left,Rght+flens --> default) Mutu Beton Ec, G, Nu juga dibiarkan default program.
Ditinjau pelat sederhana panel 6x6m, jenis two-ways berikut. Analisa dilakukan dgn program bantu SAFE, kemudian model dan properties di-export ke file S2K agar dapat dihitung dan dibandingkan hasilnya dgn SAP2000 (tidak ada modifikasi atau tambahan input). Digunakan juga pembanding dgn metode yang sederhana dan biasa banyak digunakan yaitu Tabel Koefisien Pelat PBI-71.

Perhitungan dan (Krx, Kry) elemen kolom penumpunya
Satuan (kN-m)
Luas penampang, A = 0.3*0.3 = 0.09 m^2
Inersia, Ikx = Iky = (1/12)*0.3*0.3^3 = 0.000675 m^4
Tinggi kolom, Lk = 4.0 m
Mod. Elastisitas Beton, Ec = 2.5*10^7 MPa
Kekakuan translasi
Kt = (A*Ec)/Lk = 562500 kN/m'
Kekakuan rotasi (ujung jepit)
Krx = Kry = (4*Ec*Ik)/Lk = 16875 kN.m/rad (*180/Pi <--drjt)

Pelat Lantai
Tebal, tp = 15 cm = 0.15 m
Lstrip = 3.0 m (** middle strip)
Beban Merata
- akibat berat sendiri pelat
qDead = tp*24*Lstrip = 10.8 kN/m'

Beban merata pada SAFE yang dikonversi menjadi nodal force dalam SAP2000 hasil export.
- akibat beban hidup ~400kgf/m^2
qLive = 4*Lstrip = 12 kN/m'

Kombinasi beban mati dan hidup yg ditinjau (ACI318-95)
qUlt=(1.4*qDead)+(1.7*qLive) = 35.52 kN/m'

Perhitungan momen rencana pelat (per lebar strip) pada lapangan/positif dihitung manual (dgn SpreadSheet jika node banyak)
Mlap = 7.7789+8.4742+8.9358+8.9358+8.4742+7.7789
= 50.38 kN.m

Perhitungan momen rencana pelat (per lebar strip) dihitung manual dgn Tabel koefisien momen PBI-71
- Jika ditinjau tump. elastis (Clx = 36)
Mlap_te = 0.001*qUlt*Lspan^2*Clx = 46.03392 kN.m
- Jika ditinjau tumpuan sederhana (Clx = 44)
Mlap_ts = 0.001*qUlt*Lspan^2*Clx = 56.26368 kN.m
Keadaan sesungguhnya diantara keduanya karena dimensi balok cukup besar ditambah sayap sehingga kekakuan torsinya akan menahan rotasi tumpuan. Secara konservatif misal diambil nilai tengah
Mlap_avg = (Mlap_te+Mlap_ts)/2 = 51.1488 kN.m
Sedangkan untuk Momen Negatif jepit tak terduga pada tumpuan, biasa diperhitungkan separuh momen lapangan.
Mtump = Mlap_avg/2 = 25.5744 kN.m
Dengan menggunakan koefisien maka besarnya momen tumpuan
- Jika ditinjau jepit elastis (Ctx=36)
Mtump_te = 0.001*qUlt*Lspan^2*Ctx = 46.03392 kN.m
- Jika diinjau jepit elastis (Ctx=0)
Mtump_ts = 0.001*qUlt*Lspan^2*Ctx = 0.00 kN.m
Secara konservatif juga misal diambil nilai tengah
Mtump_avg = (Mtump_te+Mtump_ts)/2 = 23.01696 kN.m
Sekedar untuk perkiraan saja, adanya hubungan antara besarnya momen positif (lapangan) & negatif (tumpuan) terhadap momen totalnya (penjumlahan absolut)
- Momen total hasil perhitungan Tabel koefisien momen PBI-71
Mtot = 51.1488+23.01696 = 74.16576 kN.m
- Momen total Hasil SAFE/SAP2000
Mtot = 31.07+50.37 = 81.44 kN.m

Momen rencana hasil program SAFE dan SP2000 terlihat selisihnya kecil, SAFE menggunakan nilai terbesar nodal reactive force pada corner nodes element shell yg ditinjau/bertemu.

Kesimpulan, kekakuan torsi balok penumpu menahan rotasi sangat berpengaruh pada distribusi momen positif dan negatif strip yang ditinjau. Pada permasalahan sederhana yg ditinjau ini, hasil tabel PBI-71 menunjukkan momen lapangan cukup mendekati dan nilainya diatas hasil program (aman). Sedangkan pada tumpuan perhitungan tabel koefisien hasilnya underestimate (tidak aman).
Lebih lanjut perlu studi penentuan kekakuan torsi balok dan kekakuan lentur kolom cara analitis/empiris, rigid zone kolom, model element solid atau sederhana dgn rigid links. Perlu juga diadakan perbandingan/selisih antara hasil force method dan moment resultant pada keadaan pelat khusus seperti yg disebutkan diawal, juga untuk jenis pelat tanpa balok (flat plate w/o drop pannel) check geser pons juga.
Selasa, 09 September 2008
Momen Rencana (Dinding) dengan mengekstrak hasil element 2D Shell
Pada keadaan tertentu penggunaan element 2D shell kadang diperlukan untuk memodelkan struktural gedung, seperti dinding geser berlubang atau tidak beraturan. Kekurangan dari penggunaan element shell yaitu hanya menampilkan hasil tegangan, tidak sesuai yg dibutuhkan untuk desain RC maka perlu perhitungan lanjut. Pada program bantu SAP2000 V8 keatas sudah tersedia post-processor tambahan untuk menentukan momen rencana yang akan digunakan dalam desain beton bertulang.
Berikut diberikan contoh sederhana pemodelan dinding dengan elemen 2D shell gaya aksial tidak ditinjau dulu untuk tujuan kejelasan penyampaian, data perhitungan :
Material Beton, Ec, G, Nu (left default)
Dimensi, BxH = 0.25x2.0m
H1 = H2 = 3.00m
Gaya horisontal
F1 = F2 = 3*10tonf = 30tonf
Sehingga :
pada elv. 3.0m
Momen, My = (F2*H2) = -90tonf.m
Geser, Vx = F2 = 30tonf
pada elv. 0.0m (dasar)
My = (F2*(H2+H1))+(F1*H1) = -270tonf.m
Vx = F1+F2 = 60tonf

Post-processor yg digunakan adalah Section Cut dan cara lain dengan semi manual (gunakan SpreadSheet+filter jika jumlah node banyak) yang mana gaya didapat dari hasil nodal reactive force (koordinat lokal) pada corner nodes element shell.
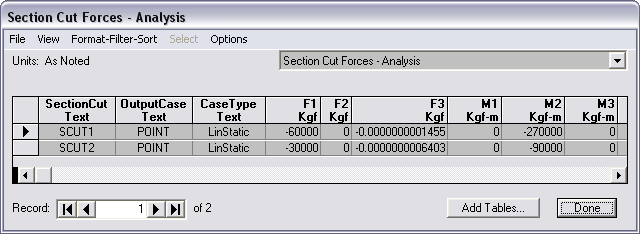
Gaya geser pada elv. 3.0m dihitung secara manual begitu juga untuk Momen yang merupakan perkalian gaya dgn jarak ke center dinding.
(untuk mencoba ketelitian digunakan satuan kgf)
V=(-4965.94)+(-9848.44)+(-9503.74)+(-5681.88)
= -30000 kgf.
M=(-44637.32*1.00)+(45030.83*-1.00)
= -89668.15 kgf.m
Hasilnya mendekati, selisih karena mesh kasar, tapi kenapa beda dgn hasil section cut ?
Lebih lanjut ditinjau juga shearwall bentuk lain seperti pd sudut bentuk L, tengah bentuk H atau U bandingkan juga dengan element frame+rigid zone. Karena pemodelan yg terakhir tsb direkomendasikan dan dianggap terbaik (Wilson, 1998). state tsb hanya untuk tinjauan 2D atau bisa juga 3D bentuk kompleks?
Berikut diberikan contoh sederhana pemodelan dinding dengan elemen 2D shell gaya aksial tidak ditinjau dulu untuk tujuan kejelasan penyampaian, data perhitungan :
Material Beton, Ec, G, Nu (left default)
Dimensi, BxH = 0.25x2.0m
H1 = H2 = 3.00m
Gaya horisontal
F1 = F2 = 3*10tonf = 30tonf
Sehingga :
pada elv. 3.0m
Momen, My = (F2*H2) = -90tonf.m
Geser, Vx = F2 = 30tonf
pada elv. 0.0m (dasar)
My = (F2*(H2+H1))+(F1*H1) = -270tonf.m
Vx = F1+F2 = 60tonf

Post-processor yg digunakan adalah Section Cut dan cara lain dengan semi manual (gunakan SpreadSheet+filter jika jumlah node banyak) yang mana gaya didapat dari hasil nodal reactive force (koordinat lokal) pada corner nodes element shell.

Gaya geser pada elv. 3.0m dihitung secara manual begitu juga untuk Momen yang merupakan perkalian gaya dgn jarak ke center dinding.
(untuk mencoba ketelitian digunakan satuan kgf)
V=(-4965.94)+(-9848.44)+(-9503.74)+(-5681.88)
= -30000 kgf.
M=(-44637.32*1.00)+(45030.83*-1.00)
= -89668.15 kgf.m
Hasilnya mendekati, selisih karena mesh kasar, tapi kenapa beda dgn hasil section cut ?
Lebih lanjut ditinjau juga shearwall bentuk lain seperti pd sudut bentuk L, tengah bentuk H atau U bandingkan juga dengan element frame+rigid zone. Karena pemodelan yg terakhir tsb direkomendasikan dan dianggap terbaik (Wilson, 1998). state tsb hanya untuk tinjauan 2D atau bisa juga 3D bentuk kompleks?
Minggu, 07 September 2008
Perbandingan Model Pertemuan Element Frame dengan Shell
Pemodelan struktural hubungan antara element frame dan shell terkadang ditemui seperti hubunganan balok lintel dengan dinding geser, efisiensi model pada pertemuan sambungan tinjauan konsentrasi tegangan, dll. Penggunaan rigid constraints adalah salah satu pilihan yg sudah tersedia pada banyak software FE seperti SAP2000.

Ditinjau struktur balok sederhana jenis kantilever seperti gambar diatas, beberapa model yang ditinjau adalah sbb:
Model 1 dihubungkan biasa, transfer gaya melalui kekakuan rotasi atau drilling DOF's pada corner nodes element shell dengan ujung element frame, tanpa adanya penghubung rigid links
Model 2 menggunakan hubungan balok yang diteruskan untuk mentransfer gaya, rigid links digunakan dan ditempatkan pada arah sejajar balok
Model 3 menggunakan hubungan rigid links yang menggunkan dan ditempatkan pada arah tinggi balok
Model 4 menggunakan hubungan balok yang diteruskan untuk mentransfer gaya, rigid links dipasang pada arah sejajar balok dan arah tingginya
Model 5 sama dengan model tiga yaitu menggunakan hubungan rigid links yang menggunakan dan ditempatkan pada arah tinggi balok, perbedaan pada penghalusan mesh pada daerah transisi
Banyak rujukan yang menyatakan perlunya menggunakan rigid link pada beberapa konfigurasi seperti pemodelan diatas, pemodelan nomer 3 dan 5 (refinement) yaitu menggunakan penghubung rigid links pada arah tinggi balok yang menunjukkan hasil yang paling mendekati.
 Lebih lengkapnya dapat dilihat/download disini.
Lebih lengkapnya dapat dilihat/download disini.
[scribd id=20839672 key=key-1km7ydpmfkkyqcs0y1gv]
Tujuan dari pemodelan tsb adalah untuk menjadikan unknow DOF's lebih sedikit sehingga analisanya efisien, tanpa kehilangan ketelitian.
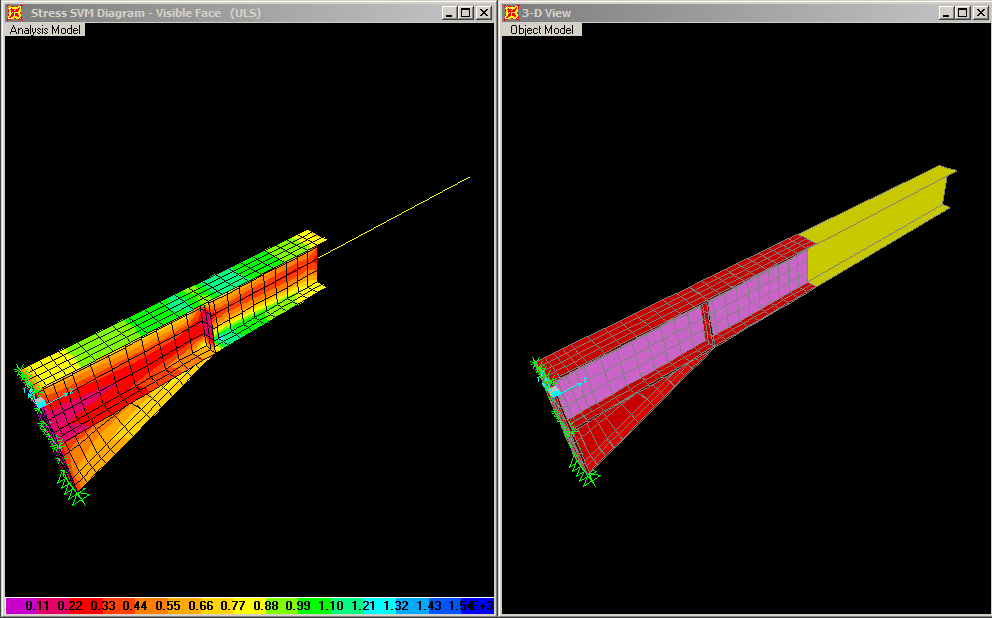
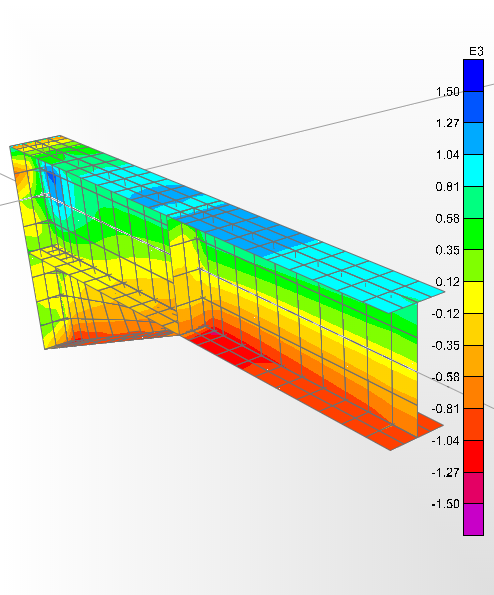
Seperti yang terlihat pada gambar diatas, contoh aplikasi peninjauan kekaukan dan distribusi tegangan pada haunched beam/stiffener.

Ditinjau struktur balok sederhana jenis kantilever seperti gambar diatas, beberapa model yang ditinjau adalah sbb:
Model 1 dihubungkan biasa, transfer gaya melalui kekakuan rotasi atau drilling DOF's pada corner nodes element shell dengan ujung element frame, tanpa adanya penghubung rigid links
Model 2 menggunakan hubungan balok yang diteruskan untuk mentransfer gaya, rigid links digunakan dan ditempatkan pada arah sejajar balok
Model 3 menggunakan hubungan rigid links yang menggunkan dan ditempatkan pada arah tinggi balok
Model 4 menggunakan hubungan balok yang diteruskan untuk mentransfer gaya, rigid links dipasang pada arah sejajar balok dan arah tingginya
Model 5 sama dengan model tiga yaitu menggunakan hubungan rigid links yang menggunakan dan ditempatkan pada arah tinggi balok, perbedaan pada penghalusan mesh pada daerah transisi

Banyak rujukan yang menyatakan perlunya menggunakan rigid link pada beberapa konfigurasi seperti pemodelan diatas, pemodelan nomer 3 dan 5 (refinement) yaitu menggunakan penghubung rigid links pada arah tinggi balok yang menunjukkan hasil yang paling mendekati.
[scribd id=20839672 key=key-1km7ydpmfkkyqcs0y1gv]
Tujuan dari pemodelan tsb adalah untuk menjadikan unknow DOF's lebih sedikit sehingga analisanya efisien, tanpa kehilangan ketelitian.

Seperti yang terlihat pada gambar diatas, contoh aplikasi peninjauan kekaukan dan distribusi tegangan pada haunched beam/stiffener.

Minggu, 24 Agustus 2008
Diagram interaksi kolom - antara hasil program, analitis dan penelitian
Tulisan ini merupakan perbandingan pembuatan diagram interaksi kolom uniaksial dan biaksial program bantu PCACOL yg menggunakan peraturan beton ACI-95 (modified phi) dengan Rujukan pustaka dari materi kuliah saya yg menggunakan peraturan beton SNI-91, dulu sudah pernah dilakukan beberapa pada kolom uniaksial pada kesempatan ini ditambahkan perbandingan kekuatan kolom biaksial motode kontur Bresler pada kolom bentuk persegi dan perbandingan dgn hasil penelitian pada kolom biaksial bentuk L.

Pada perbadningan kolom biaksial persegi metode Bresler terlihat perbadaan yg cukup signifikan akibat penentuan konstanta m&n, sedangkan pada perbandingan kolom biaksial bentuk-L dgn penelitian terlihat pada P>40% hasilnya cukup mendekati, berbeda dgn keadaan P kecil perbedaanya cukup signifikan.
 lebih jelasnya dapat dilihat/download disini.
lebih jelasnya dapat dilihat/download disini.
[scribd id=20840207 key=key-tutxwjvc6v9y7i96lbk]

Pada perbadningan kolom biaksial persegi metode Bresler terlihat perbadaan yg cukup signifikan akibat penentuan konstanta m&n, sedangkan pada perbandingan kolom biaksial bentuk-L dgn penelitian terlihat pada P>40% hasilnya cukup mendekati, berbeda dgn keadaan P kecil perbedaanya cukup signifikan.
[scribd id=20840207 key=key-tutxwjvc6v9y7i96lbk]
Langganan:
Komentar (Atom)