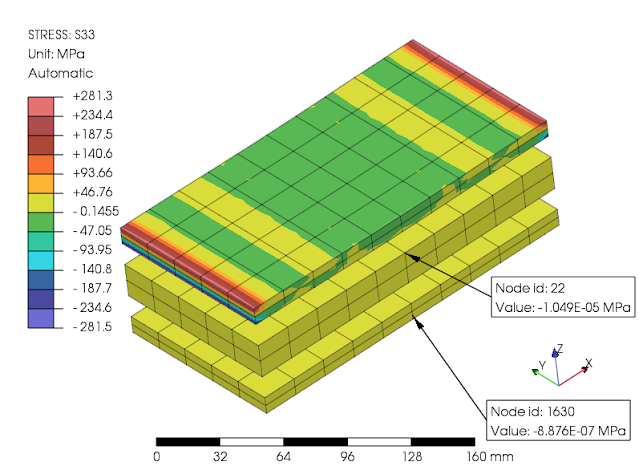
material dgn kepemilikan nol atau kosong dlm FE

material dengan kepemilikan nol (null) atau kosong (void) tersedia pada software LS Dyna dan OpenRadioss, ini merupakan kebalikan dari material sangat kaku (rigid) yg ada. Program bantu elemen hingga CalculiX tidak menyediakan jenis tersebut, sebagai penggantinya digunakan pendekatan dengan nilai pembagi (null/void) atau pengali (rigid) sebesar 1.0x10^9 pada nilai kepemilikan material terutama modulus elastisitas seperti contoh berikut. Terlihat deformasi menunjukan suatu besaran pada post-processor karena kesebandingan defleksi node mesh yg bertemu, sedangkan nilai tegangan tetap menunjukan hasil yg mendekati nol yg berarti sudah sesuai dapat mewakilkan. Untuk menghindari averaging pada proses extrapolated dari integration point suatu elemen, maka model dibawah ini dibagi menjadi tiga group atau part dan node antar permukaanya dihubungkan dengan tie constraints.

.

.

.

.

.

.

.

penggunaan nilai modulus elastisitas yg sangat rendah dan hampir nol tersebut perlu dengan perhatian (caution), karena perbedaan selisih  kekakuan elemen yg bertemu dapat saja menjadikan solver gagal akibat ill-conditioned. Hal tersebut dapat dihindari dengan meningkatkan  nilainya jika terlalu kecil, namun solver CalculiX kelihatannya cukup baik menyelesaikan tanpa kendala. Batasan lain kondisi adalah tidak dapat diterapkannya beban muka elemen solid atau beban titik pada node elemen dgn material null tersebut, karena kekakuannya hampir tidak ada maka cenderung akan menjadikan pergerakan benda kaku (rigid body motions).

.

.

model diatas adalah dengan menggunakan elemen shell akan diterapkan beberapa lapis juga, namun untuk awal sebagai perbandingan tidak ada.

,

.

.

.

.

berikut model dengan elemen shell composite, ada yg tidak sesuai pada defleksi dan tegangan pelat bagian bawah, walau hasil bagian tengah void sudah sesuai pada  tegangan yg  bernilai mendekati nol.

.

,

.

.

sebagai perbandingan tambahan dibuat model penampang box hollow, juga untuk model elemen solid dimana lubang dimodelkan secara langsung. Hasil analisa menggunakan elemen solid lebih besar secara umum dengan perbedaan yg cukup signifikan.

.

.

.

.

.

.

.

.

.

.

.

.

.

Read More

pilih elemen klasik atau kontinum?

kebanyakan program elemen hingga untuk tujuan desain (linear elastis) saat ini seperti SAP/ETABS, STAAD, RISA, Robot SA, dll hanya menggunakan formulasi klasik atau konvensional untuk elemen 1D balok (beam) dan 2D pelat//cangkang (shell). Namun program advanced seperti Abaqus dan Ansys menyediakan jenis kontinum, biasa dinamakan solid-shell yg mana ketelitian dan kecepatan diantara elemen shell dan solid. CalculiX secara khusus tidak mempunyai jenis elemen tersebut, namun serara langsung menerapkan jenis elemen solid murni dan penggunaan constraint pada saat expansi. Jika unuk tujuan desain maka elemen dengan formulasi standar, klasik atau konvensional biasanya sudah mencukupi, namun untuk tujuan investigasi kapasitasnya dengan analisa nonlnear maka jenis kontinum dianjurkan. Secara prinsip elemen solid lebih baik karena tegangan tiga dimensi ditinjau langsung tanpa suatu pendekatan (degenerates), namun dapat saja ada masalah locking pada element daerah tertentu karena deformasi yg cukup exstrim.

.

(source:  Peeters etal, 2018)

,

pertimbangan yg paling mencolok adalah kebutuhan komputasi pada hardware dan waktu penyelesaian, seringkali jumlah node yg sangat banyak tidak dapat diselesaikan karena keterbatasan spesifikasi komputer yg digunakan. Seperti contoh grafik diatas, rasio mendekati 1:10 antara penggunaan shell dengan solid, namun jika akurasi adalah lebih utama maka banyak merekomendasikan jenis solid-shell atau solid murni. Dominan kemampuan hardware adalah pada jumlah memory RAM tertanam, namun saat ini tanpa perlu high performance HPC spesifikasi komputer Mini-PC sudah banyak beredar dengan kapasitas RAM sebesar 16Gb dan 32Gb, laptop dengan kapasitas 8Gb dan 16Gb juga.  Reduksi jumlah nodes tanpa perlu kehilangan akurasi masih dapat dijangkau dengan penggunaan elemen jenis quadratic dengan mesh yg kasar secara umum dan penghalusan tambahan pada daerah khusus. Langkah lain adalah memecah model menjadi global kesulurhan dan lokal setempat dengan fungsi Sub-Model. Investasi kepada software atau hardware adalah pilihan masing-masing, namun untuk saya adalah yg terakhir. Kelebiihan dan kekurangan antara elemen shell formulasi klasik atau konvensional dan solid banyak dijelaskan banyak arikel dibawah mengenai topik solid-shell, dapat digunakan untuk menghindari pitfall analisa perilaku struktural berbantu elemen hingga program CalculiX yg composed atau OpenSees yg layered/fiberized. Selain karena alasan keterbatasan tidak memiliki elemen jenis solid-shell, biasanya software opensource menyerahkan kepada pengguna untuk verifikasi secara mandiri, walau sebagian mungkin sudah ada melalui publikasi resmi.

• The challenge of a three–dimensional shell formulation - the conditioning problem, Wolfgang A. Wall, Michael Gee and Ekkehard Ramm, 2000 (link)
• Solid-shell approach based on first-order or higher-order plate and shell theories for the finite element analysis of thin to very thick structures, Guoqiang Wei, Pascal Lardeur, Frédéric Druesne, 2024 (link)
• Quadratic solid-shell elements for nonlinear structural analysis and sheet metal forming simulation, Peng Wang, Hocine Chalal, Farid Abed-Meraim, 2017 (link)
• Stress–displacement stabilized finite element analysis of thin structures using Solid-Shell elements, Part II: Finite strain hyperelasticity, A. Aguirre, R. Codina, J. Baiges, I. Castañar, 2024 (link)
• Benchmarking Computational Shell Models, Petr Krysl & Jiun‑Shyan Chen, 2022 (link)
• A Selection of Benchmark Problems in Solid Mechanics and Applied Mathematics, Jörg Schröder,  Thomas Wick, Stefanie Reese, Peter Wriggers, Ralf Müller, Stefan Kollmannsberger, Markus Kästner, Alexander Schwarz, Maximilian Igelbüscher, Nils Viebahn, Hamid Reza Bayat, Stephan Wulfnghof, Katrin Mang, Ernst Rank, Tino Bog, Davide D’Angella, Mohamed Elhaddad, Paul Hennig, Alexander Düster, Wadhah Garhuom, Simeon Hubrich, Mirjam Walloth, Winnifried Wollner, Charlotte Kuhn,  Timo Heister, 2020 (link)
• Plastic buckling and collapse of thin shell structures, using layered plastic modeling and co-rotational ANDES finite elements, Nélvio Dal Cortivo, Carlos A. Felippa, Henri Bavestrello, William T.M. Silva, 2009 (link)
• A nine nodes solid-shell finite element with enhanced pinching stress, Mouhamadou Dia, Nahiene Hamila· Mickaël Abbas· Anthony Gravoui, 2021 (link)
• Solid or shell finite elements to model thick cylindrical tubes and shells under global bending, A.J. Sadowski & J.M. Rotter, 2013 (link)
• Comparison of Shell and Solid Finite Element Models for the Static Certification Tests of a 43 m Wind Turbine Blade, Mathijs Peeters, Gilberto Santo, Joris Degroote and Wim Van Paepegem, 2018 (link)
• Application of the continuum shell finite element SHB8PS to sheet forming simulation using an extended large strain anisotropic elastic-plastic formulation, Abdellah Salahouelhadj, Farid Abed-Meraim, Hocine Chalal, Tudor Balan, 2013 (link)
• A Continuum Based Solid Shell Element Based on EAS and ANS, Waleed Ahmad Mirza, 2015 (link)
• Investigation of finite element (FE) modelling of composite materials: shell, solid and solid layered composite modelling – Comparison of impact on simulation results., Katarzyna Gojny,  Adam Dacko, 2021 (link)
• Extension of the `solid-shell' concept for application to large elastic and large elastoplastic deformations, R. Hauptmann, K. Schweizerhof and S. Doll, 2000 (link)
• 3D-shell elements for structures in large strains, Theodore Sussman, Klaus-Jürgen Bathe, 2013 (link)
• Development of solid-shell elements for large deformation simulation and springback prediction, Nhu Huynh Nguyen, 2009 (link)
• Benchmark Computations of low and high order Shell Elements on adaptively generated FE Meshes, S. Kizio, K. Schweizerhof, A. Düster, E. Rank, 2006 (link)
• Critical examination of benchmark problems for large rotation analysis of laminated shells. I. Kreja, 2006 (link)
• Popular Benchmark Problems for Geometric Nonlinear Analysis of Shells, K.Y. Sze1, X.H. Liu, S.H. Lo, 2004 (link)
• New quadratic solid-shell elements and their evaluation on linear benchmark problems, Farid Abed-Meraim, Vuong-Dieu Trinh, Alain Combescure, 2013 (link)
• Simulation of nonlinear benchmarks and sheet metal forming processes using linear and quadratic solid‒shell elements combined with advanced anisotropic behavior models, Peng Wang, Hocine Chalal and Farid Abed-Meraim, 2016 (link)
• New quadratic solid-shell elements and their evaluation on popular benchmark problems, Farid Abed-Meraim, Vuong-Dieu Trinh, Alain Combescure, 2017 (link)
• A new feature to model shell-like structures with stacked elements, Tobias Erhart, 2015 (link)
• Towards overall adaptive modeling based on solid-shell and solid-beam approaches for the static and dynamic finite element analysis of structures, Guoqiang Wei, 2022 (link)
• A mixed shell formulation accounting for thickness strains and finite strain 3d-material models, S. Klinkel, F. Gruttmann, W. Wagner, 2006 (link)
• An improved assumed strain solid–shell element formulation with physical stabilization for geometric non-linear applications and elastic–plastic stability analysis, Farid Abed-Meraim and Alain Combescure, 2017 (link)
• New prismatic solid-shell element: Assumed strain formulation and evaluation on benchmark problems, Farid Abed-Meraim, 2008 (link)
• Layered solid-shell elements for accurate prediction of stresses in laminated composites, Elias Borjesson, 2016 (link)
• Investigation of finite element (FE) modelling of composite materials: shell, solid and solid layered composite modelling – comparison of impact on simulation results, Katarzyna Gojny, Adam Dacko, 2020 (link)

catatan : program CalculiX juga menyediakan elemen 1D (beam) dan 2D (shell) dengan formulasi klasik atau konvensional yg sudah terbaru updated berikut perbaikannya namun jenis analisa yg didukung masih terbatas statis dan linear elastis, small deformation.

Read More

model balok beton bertulang dgn elemen shell (composite)

sebelumnya telah dibahas mengenai pendekatan pemodelan pelat beton bertulang dengn menggunakan elemen shell dan fungsi composite pada CalculiX. Balok beton bertulang juga masih memungkinkan menggunakan metode pendekatan model tersebut, perbedaan yg lebih terlihat adalah adanya sengkang tertutup untuk tahanan geser dan pengekangan beton bagian dalam atau inti (core).

.

.

hal lain yg berbeda adalah pada pemisahan kelompok bagian tulangan pokok sesuai jumlahnya dalam satu lapis. Kelebihan pemodelan dengan menggunakan elemen shell continuum pada CalculiX adalah dapat digunakannya untuk model balok tinggi (deep beams) dengan dan tanpa adanya bukaan (void). Balok dengan sayap juga dapat dimodelkan, untuk pertemuan sisi vertikal (webs) dan horisontal 9flanges) secara otomatis akan dihubungkan dengn knot yg menjaga kompatibilitasnya. Balok lebar dan tebal (wide beams) terhadap gaya torsi juga dapat digunakan karena secara aktual shell elemen di CalculiX adalah solid setelah expansi. Perbedaan penggunaan diameter yg ada akan menjadi sedikit kendala karena layer yg digunakan mempunyai ketebalan sama tiap lapisnya, untuk itu lebar pada partisi garis perlu menggunakan equivalensinya dengan acuan luas penampang yg tetap sama.

.

.

.

.

.

.

.

diatas adalah hasil dari material yg masih linear elastis, perbedaan material tiap lapis belum diterapkan sebab jumlah lapis hanya satu. Berikut hasil dengan penerapan jumlah empat lapis namun material masih sama tiap lapisnya. 

.

.

.

.

.

.

berikut telah dditerapkan perbedaan material tiap lapisynya, namun material beton dan baja masih elastis linear. Tulangan pokok bagian atas adalah 4btg dan 2btg, sedangkan bagian bawah adalah 2btg.

.

.

.

.

.

.

.

Read More

model pelat beton bertulang dgn elemen shell (composite)

beton bertulang merupakan struktur komposit, gaya tekan ditahan oleh material beton sedangkan gaya tarik oleh baja Mengenai gaya geser dan torsi, sebagian atau sepenuhnya ditahan oleh beton namun sesuai kapasitas dan selebihnya tulangan baja tambahan untuk itu.  Pemodelan menggunakan elemen solid masih memungkinkan namun untuk jenis pelat atau cangkang beton bertulang yg biasanya pola pembesian masih cukup seragam, maka pemodelan menggunakan elemen shell continuum dan fungsi composite pada CalculiX akan cukup membantu mempercepat dan menyederhanakannya. Elemen shell pada CalculiX akan dilakukan expansi tetap menjadi elemen solid dengan penerapan multi point constraint pada tumpuan atau beban dan integrasi numerik antar lapisnya, dilakukan secara internal oleh solver dan otomatis. Hal tersebut tentunya memberikan kelebihan karena pengaruh tegangan tiga dimensi terutama masalah geser pons dapat lebih mewakilkan, dimana hal tersebut diabaikan dalam formulasi elemen shell jenis klasik atau konvensional. Nonlinearitas material untuk baja dan beton dapat diterapkan setiap lapisnya sehingga perilakunya akan dapat lebih mendekati.

.

.

hal pertama yg dilakukan adalah melakukan partisi geometry membagi menjadi tiga yaitu beton, baja tulangan (jarak dan dimensi equivalen) dan beban terpusat (parsial merata). Contoh berikut adalah pelat dengan tumpuan sederhana dimodelkan seperempat karena kondisi simetris. Dimensi pelat adalah 1400mm panjang dan tebal 100mm, strip tulangan baja sebesar 20mm.  Jika terdapat perbedaan diameter tulangan perlu dibuat equivalensi lebar strip dengan kesebandingan luasan, disebabkan ketentuan mengenai ketebalan suatu lapisan (layer) adalah seragam atau sama tebalnya.

.

.

.

berikut hasil sebelum diterapkan fungsi composite, tidak menggunakan beberapa jumlah lapis pada ketebalan pelat, material juga masih asumsi elastis. Elemen shell jenis quadratic (S8 & S6). Perbedaan material tiap lapis pada jalur area tulangan belum diterapkan.

.

.

.

dibawah diterapkan jumlah lapis empat, material yg ditentukan tiap lapisnya masih sama dgn sebelumnya. Elemen shell jenis quadratic (S8R & S6)

.

.

.

.

.

berikut hasil diterapkan jumlah lapis delapan dan juga perbedaan material yg ditentukan, untuk lebih mendekati lagi maka jarak pusat tulangan ke tepi luar permukaan pada arah sumbu-X dan sumbu-Y perlu dipisah partisinya dan menyesuiakn kondisi aktual urutannya. 

.

,

.

.

.

model diatas masih dalam kondisi linear elastis pada beton, berikut menggunakan material Compression_Only pada CalculiX. Hasilnya memperlihatkan tegangan leleh kriteria von Mises pada baja tulangan sisi bawah meningkat sekitar 3 (tiga) kalinya lebih dari sebelumnya.

.

.

.

.

.

.

untuk lebih teliti maka penggunaan material baja berikut plastisitas perlu digunakan, model lain material beton plastis seperti DruckerPragerCap atau kerusakan (damage) seperti Mazars dapat cukup mudah definisinya dengan meberikan blok data material dan menerapkannya sesuai lapis pada pilihan composite. Kendala penggunaan material plastis atau damage biasanya pada masalah konvergensi solver, penggunaan beban adalah deleksi mungkin akan membantu atau memang beban permukaan yg diterapkan terlalu besar.. Seperti berikut, iterasi terhenti pada last step 13 tidak dapat dilanjutkan karena masalah konvergensi, hasil terakhir sebelum gagal tersebut untuk deformasi lendutan dapat digunakan sebagai acuan penentuan beban defleksi selanjutnya.

.

.

.

.

.

.

Read More