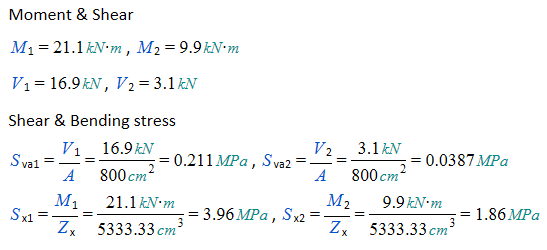.
.
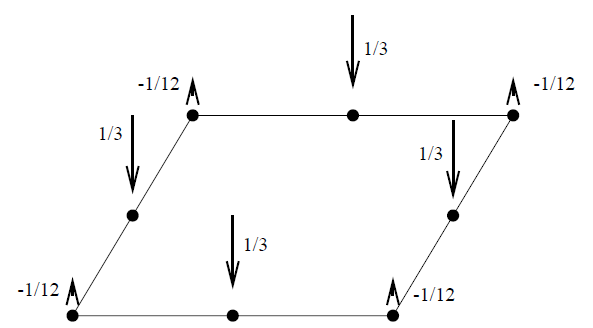
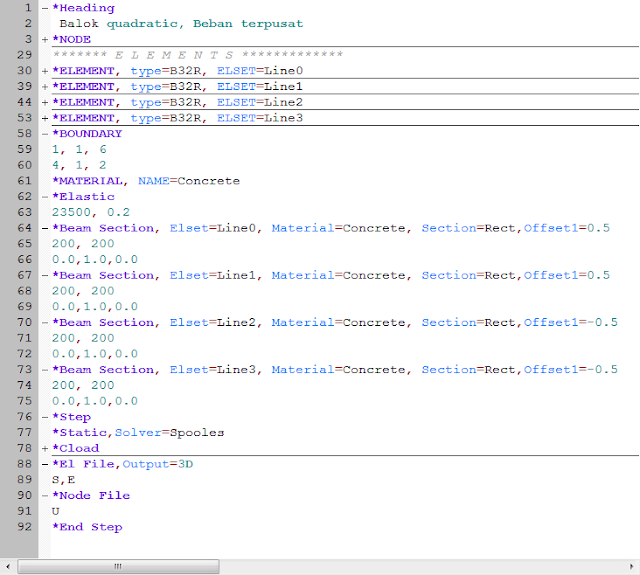
pada beberapa posting sebelumnya membahas konversi beban titik dari beban merata pada balok, namun ini terlihat hanya berlaku pada jenis elemen linear. Pada tulisan ini ditinjau khusus untuk jenis quadratic element seperti balok pada CalculiX yaitu B32/B32R, pelat atau shell S8/S8R yg mana pada tahap perhitungan oleh solver akan dilakukan expansi menjadi elemen hexahedral quadratic (C3D20/C3D20R). Penempatan beban muka juga akan berpengaruh, misal pada sisi muka atas bagian penampang balok saja, bagaian bawah, atau disebarkan pada kedua sisinya.
.
.
.
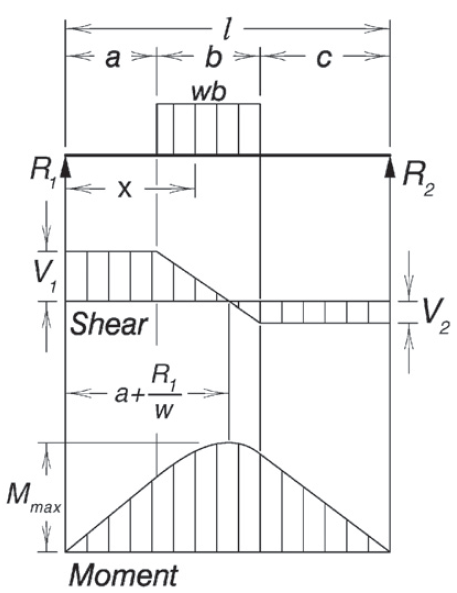
pada cara analitis sperhitungan tangan rujukan AISC tersebut diatas tidak diberikan rumusan perhitungan lendutan, sebagai tambahan perbandingan digunakan software analisa struktur lain yaitu Ftool dari Tecgraf/PUC-Rio.
.
.
ditinjau balok dengan beban parsial ditengah bentang seperti contoh diatas, material beton dan akan ditinjau terhadap berbagai kondisi tumpuan lain juga dengan software analisa struktur.
.
.
.
.
berikut penggunaan elemen shell (S8/S8R) yg juga diterapkan layering sebanyak dua buah elemen pada sisi ketebalan. Diterapkan beban adalah pada permukaan bagian atas dan model lain dengan beban titik nodal, terlihat hasilnya masih identik atau sama.
.
.
.
.
.
.
model beban terpusat untuk penggunaan elemen shell hasilnya menunjukkan hampir sama atau identik dengan hasil pada elemen solid, berikut dibawah juga hasilnya sama saat digunakan elemen beam. Perbedaan metode pilihan beban merata dan terpusat yaitu pada analisa large deformation, beban muka akan mengikuti (load follower) pergerakan part sedangkan terpusat tidak. Pada beban merata muka elemen maka bersifat sama nilainya pada titik semua sudut, sedangkan untuk beban terpusat titik nodal dapat tidak merata. Hal ini dapat berguna misal untuk beban permukaan berbentuk segitiga, trapesium dan mungkin sembarang seperti kurva parabolik mengikuti fungsi tanpa perlu pendekatan nilai rata-ratanya.
.
.
.
.
.
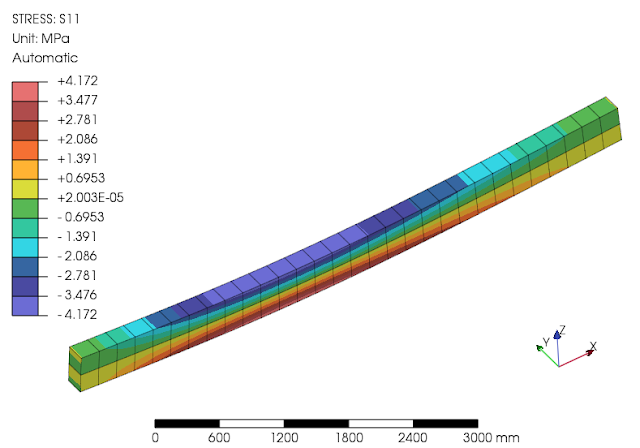
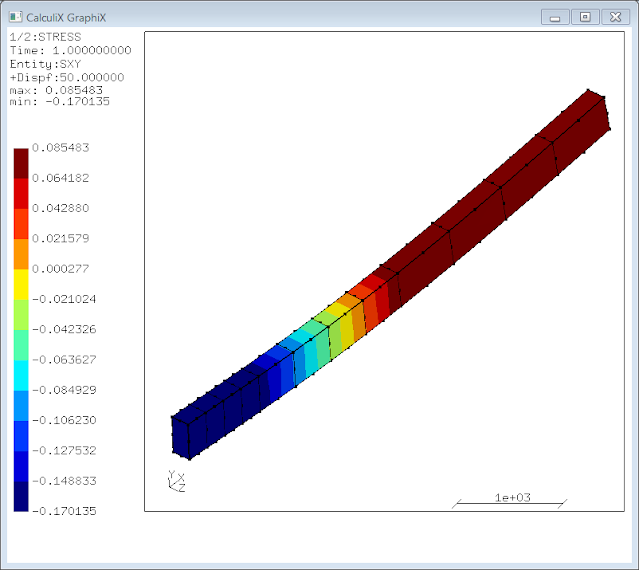
dicoba kondisi tumpuan lain yaitu sisi kiri adalah tumuan jepit (fixed), terlihat hasilnya masih konsisten dengan artian penerapan konversi beban dari merata menjadi beban titik dapat digunakan pada berbagai keadaan. Mengenai hasil tegangan lentur nilainya mendekati, sedangkan tegangan geser adalah nilai rata-rata, nilai defleksi 2.46% lebih besar.
.
.
.
.
.
.
fungsi atau feature untuk layering mementukan jumlah elemen pada ketebalan atau ketinggian balok (beam) belum didukung oleh CalculiX, untuk itu ada cara lain dengan duplikasi elemen berikut penerapan offset. Metode atau cara tersebut kurang dianjurkan karena menambahkan ikatan simpul node atau knot, terlihat hasilnya lebih kaku senilai 7.76% besarnya.
.
.
.
jika ingin tetap menggunakan cara perbaikan model seperti diatas maka nilai modulus elastisitas perlu direduksi agar hasilnya mendekati, misal sebagai berikut setelah diturunkan sebesar 10% nilainya. Hal ini diperlukan saat ditempuh analisa dengan large deformation diaktifkan dan juga plastisitas material juga ditinjau.
.
.
.