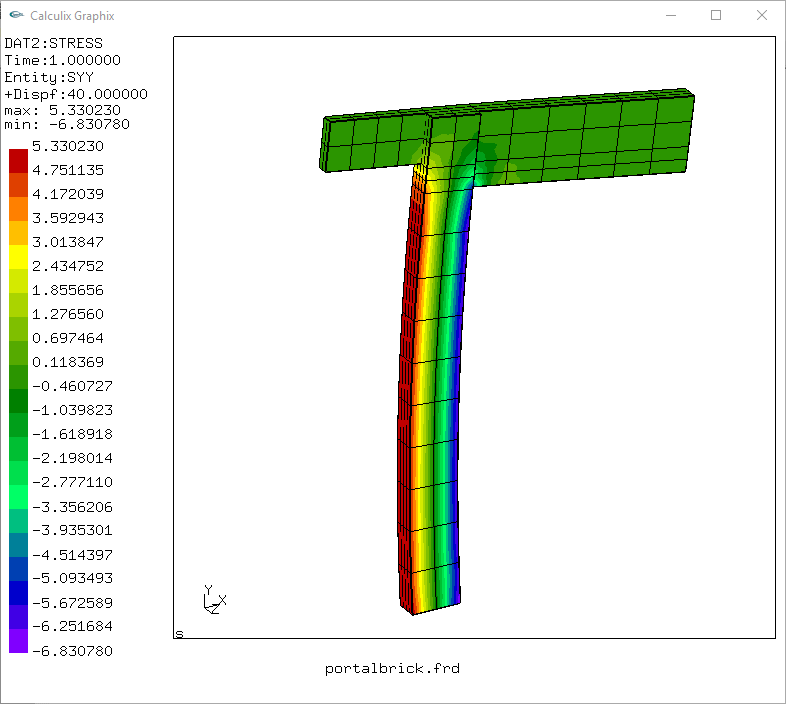
masalah nonlinear yg paling sederhana adalah adanya batasan elemen (truss) dari kemampuan yang hanya menerima tarik atau tekan, dapat juga ditentukan elemen hanya tarik namun mempunyai sedikit batasan tekan atau kondisi sebaliknya. pada penggunaan software sya sebelumnya SAP yaitu dikenal dengan frame with tension only atau compression only. elemen frame jenis tension only biasa digunakan pada komponen gedung untuk bracing, namun pengguna dapat memberikan suatu nilai kecil batasan jika diinginkan mempunyai kemampuan tekan. saya tertarik mencari rujukannya, misal untuk jenis brace tsb atau frame dgn tension only maka analisa adalah nonlinear dilakukan secara bertahap atau iterasi, jika pada tahap pertama terdeteksi adanya suatu brace yg mengalami nilai tekan diatas yg ditentukan maka akan dianggap tidak ada pada tahap analisa berikutnya dst.

berbeda dgn program FE nonlinear, umumnya yg diutamakan adalah perilaku nonlinear materialnya. untuk material yg dominasi kemampuannya tekan dan getas maka akan banyak pilihan pada program advanced FE seperti adanya jenis nonlinear material Mohr Coulomb atau Drucker Prager yg biasa diaplikasikan untuk pemodelan pondasi atau dinding penahan tanah dan pemodelan beton bertulang. jenis material elasto-plastis yg lebih sederhana dari kedua material elasto-plastis diatas adalah Compression_Only material yg sudah tersedia pada program elemen hingga CalculiX versi 2.8 keatas.

perbandingan kurva diatas dengan material beton hasil pengujian tegangan biaxial dari Kupfer (1973) yg sya ambil dari paper Como etal (2007) ada sedikit perbedaan dimana pada tegangan tekan biaxial maka kemampuannya akan meningkat sampai sekitar 25% dari kondisi tegangan uniaxial.

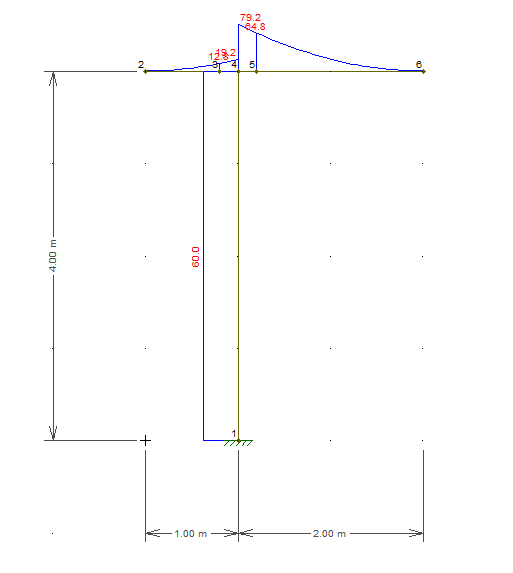
disini saya mencoba meninjau secara singkat dan belum sampai ke perbandingan pendekatan secara teoritis, contoh adalah balok beton bertulang (bxh=20x40cm) kantilever (l=2.0m) dengan beban merata pada permukaan atas. mutu tekan beton (fc=30MPa) kapasitas tegangan tarik material ditentukan sebesar 10% dari kapasitas tegangan tekan umumnya. mutu tekan beton tsb dalam hal ini hanya sebagai acuan tidak berpengaruh pada analisa dgn elemen hingga menggunakan material Compression_Only.
tulangan dimodelkan dengan elemen truss (T3D2) mengunakan material yg masih elastis, hubungan dengan node elemen solid beton dianggap monolit sempurna.
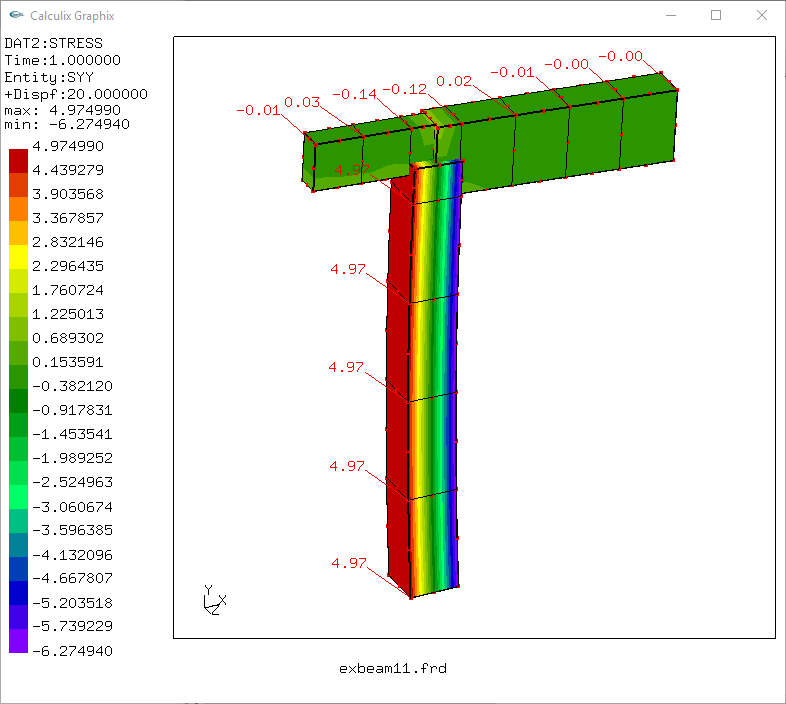
deformasi,


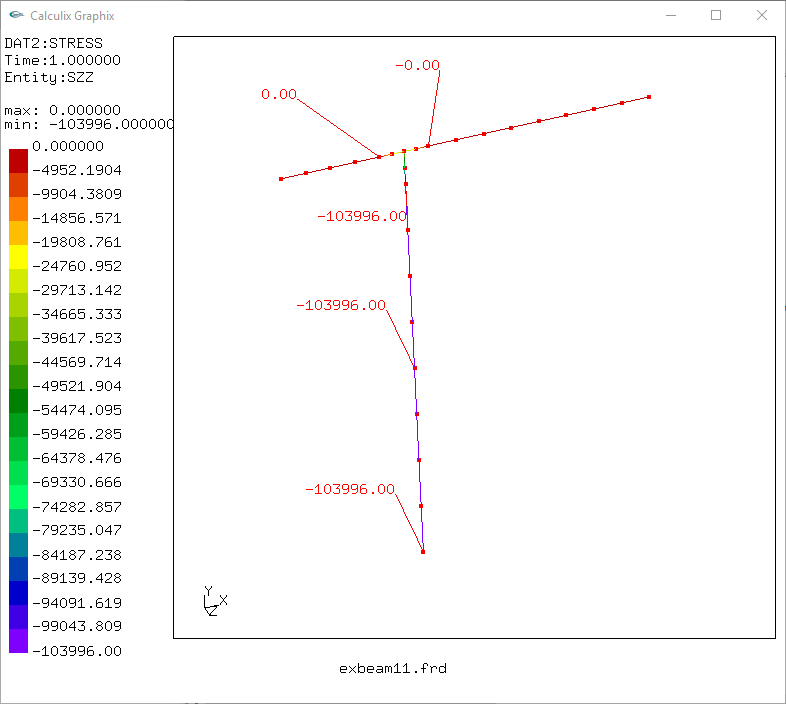
tegangan lentur,

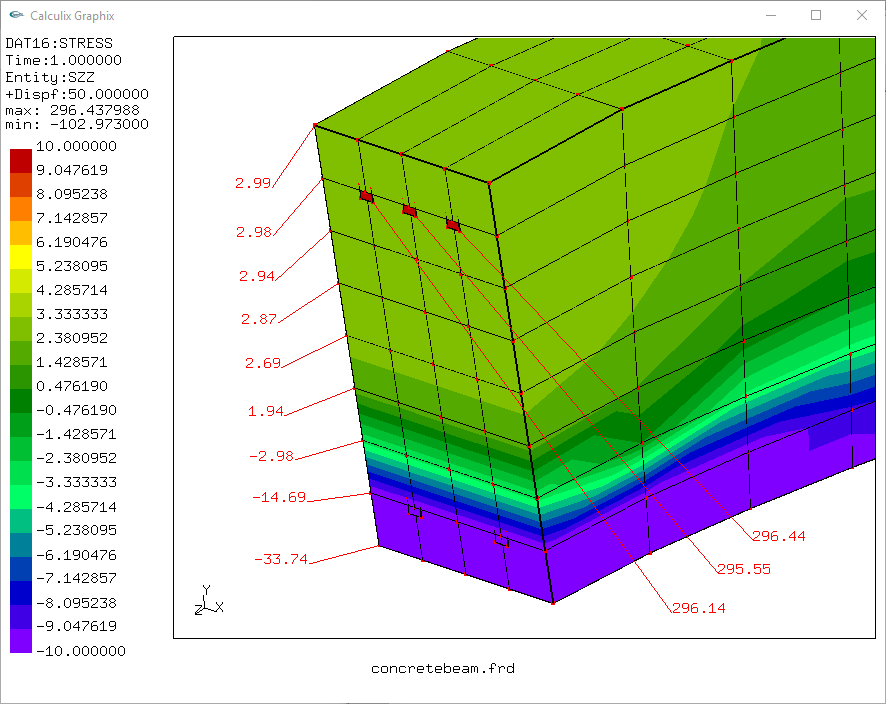
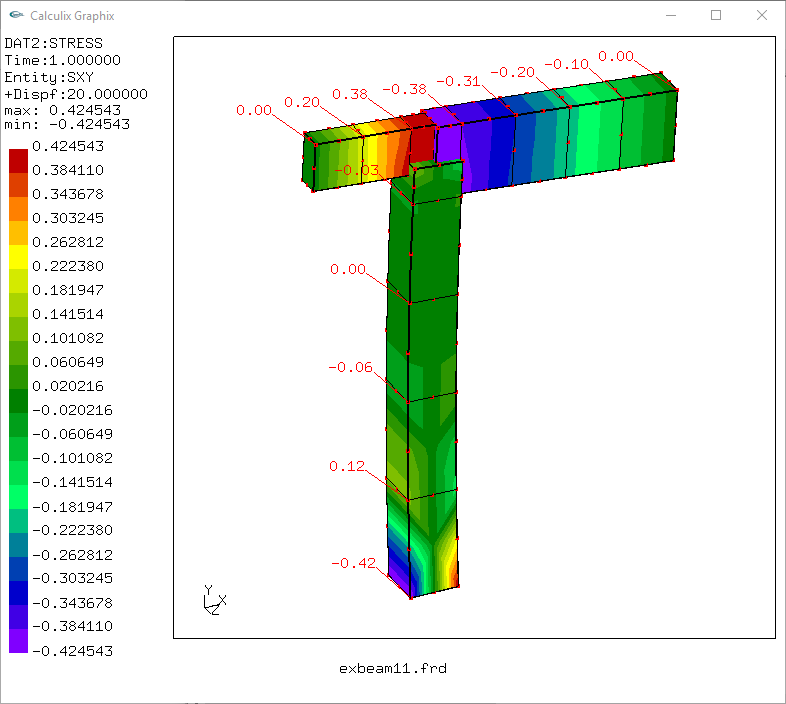
tegangan geser,

walau belum dilakukan validasi atau verifikasi namun sekilas hasil dan perilaku menunjukkan seperti yg diperkirakan. tegangan tarik sebagian besar diterima oleh tulangan atas, sedangkan tegangan geser hanya diterima pada balok yg mengalami tekan (tidak retak). masih ada beberapa yg belum sesuai, diantaranya adalah sisi tumpuan bagia atas yg mengalami tarik seharusnya sudah retak dan kemudian tegangan tarik diterima penuh oleh tulangan.
dibawah dicoba dengan mengabaikannya kapasitas tarik material pada elemen solid balok beton, ditentukan nilai hanya sebesar 1% kuat tekannya. dan hasilnya menunjukan sebagai berikut,

terlihat saat mengabaikan kemampuan tarik material beton menjadikan tegangan tarik baja tulangan atas dan tegangan tekan balok beton sisi bawah meningkat cukup signifikan.
*updates
model balok diatas menggunakan material beton elasto-plastis kriteria Modified Mohr Coulomb (Abaqus UMAT by J. Clausen, 2006)
defleksi,

tegangan lentur,


tegangan geser,

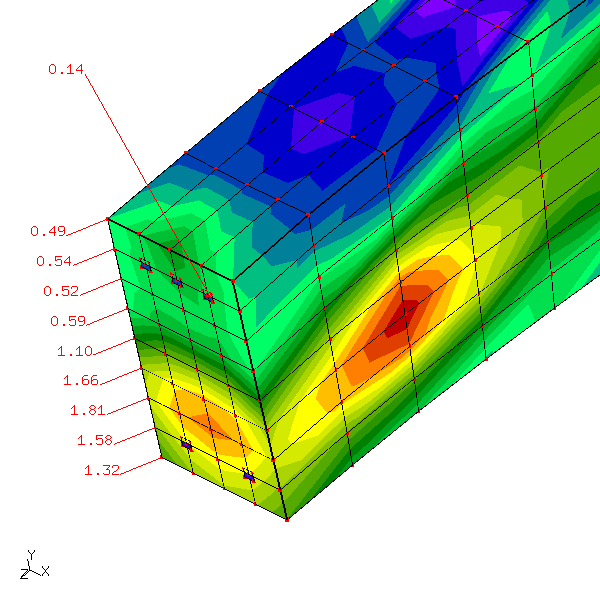
perlu model yg lebih realistis yaitu representasi tulangan dengan elemen solid, ditambahkannya pengaruh tahanan geser dan kekangan dari tulangan sengkang. juga pelu diterapkan nonlinearitas materil baja tulangan tersebut. lainnya yg tidak boleh terlewat adalah perbandingan dengan analisa secara pendekatan teoritis perhitungan tangan sebagai acuan awal.
**updates
model diatas agak rumit terutama saat pemodelan tulangan sengkang, sya coba model yg lebih sederhana untuk mencari perkiraan awal perbedaan pemodelan tulangan pokok dengen elemen truss (t3D2) dan full solid. ditinjau balok 50x150mm panjang 500mm. material hanya tekan (kapasitas 10%), beban merata.
lendutan,

tegangan lentur,


tegangan geser,


terlihat hasilnya mendekati, dapat diartikan model tulangan pokok dgn elemen truss (T3D2) dapat digunakan untuk memprediksikan awal. perbaikan model tetap diperlukan seperti model tulangan dgn elemen solid, diikut sertakannya model tulangan sengkang dan kriteria elasto-plastis materialnya.
***updates
model balok beton bertulang sederhana diatas menggunakan material elasto-plastis kriteria Modified Mohr Coulomb (Abaqus UMAT by J. Clausen, 2006)

defleksi,

tegangan lentur,


tegangan geser,
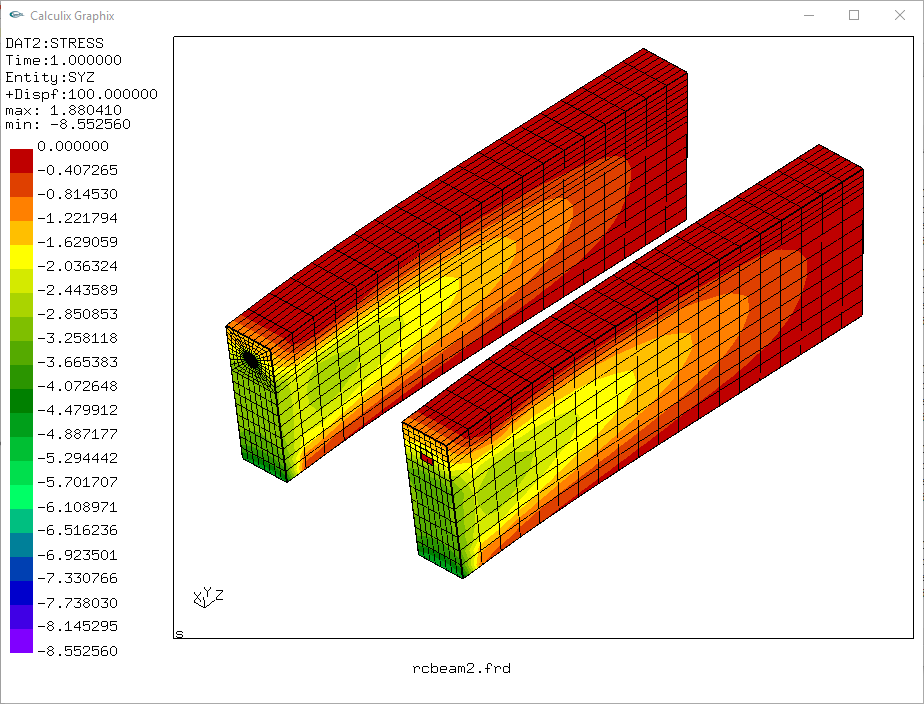

tegangan tarik pada balok beton yg terjadi pada sisi atas masih cukup besar, ini kemungkinan besar disebabkan dari penentuan nilai parameter dari material modified MC yaitu angle of internal friction, dilatancy dan cohesion. perlu dicari rujukan dalam penentuan nilai tersebut hubungannya dengan mutu tekan beton (?)

menggunanakan parameter nilai kohesi (c=3.0 N/mm^2) sedangkan nilai lainnya tetap.
lendutan,
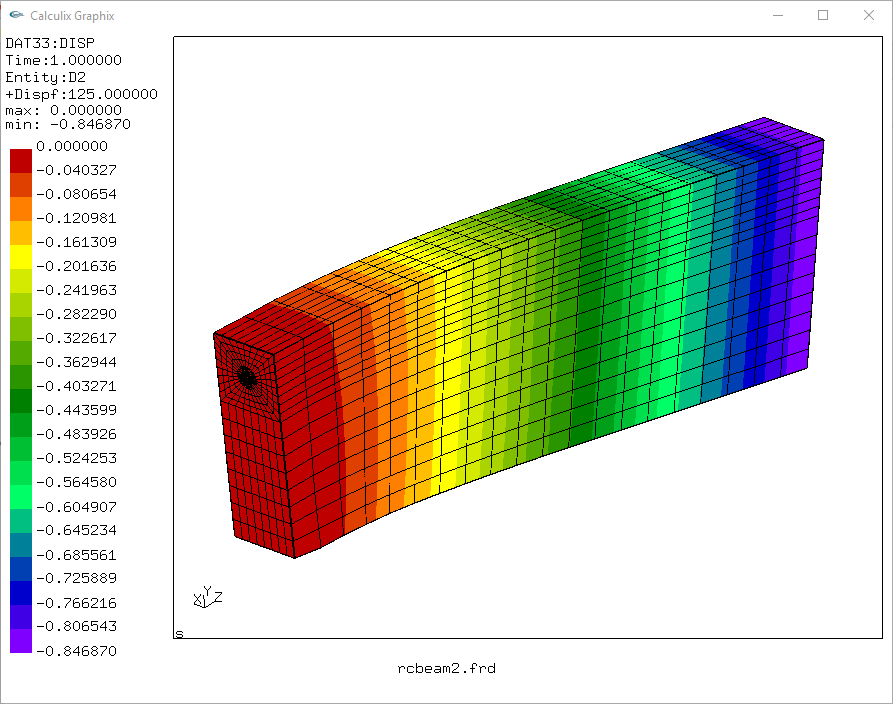
tegangan lentur,
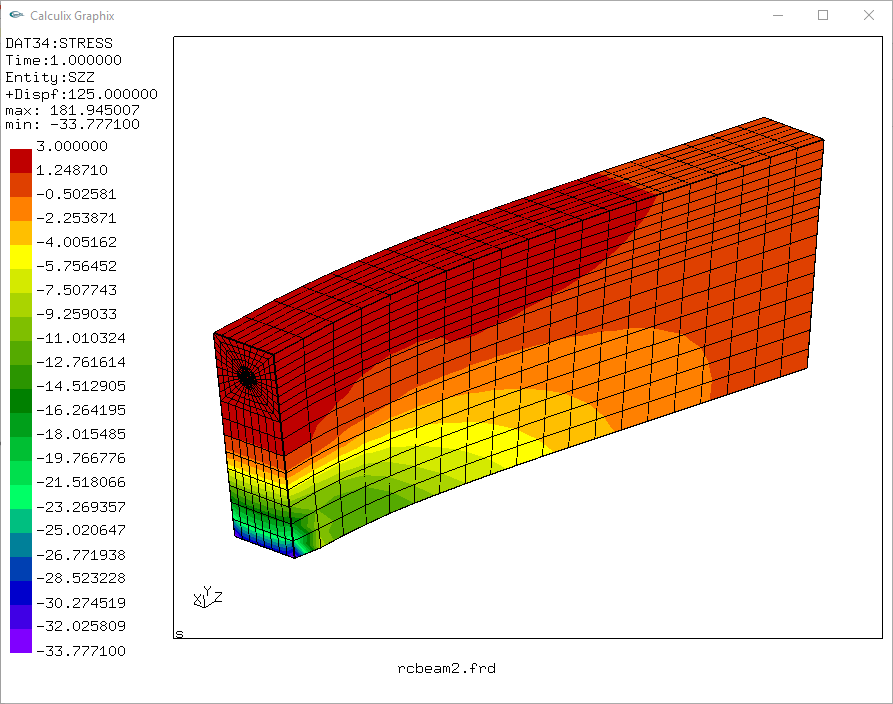
penekanan tampilan warna batas/kontur sisi bawah - tegangan tekan,

penekanan tampilan warna batas/kontur sisi atas - tegangan tarik,

tegangan geser,
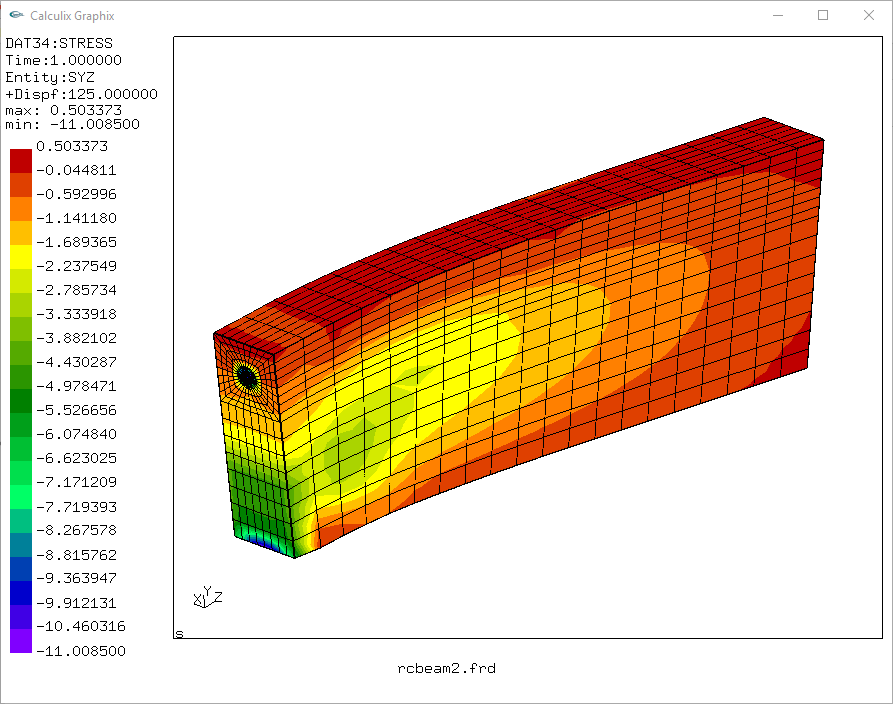
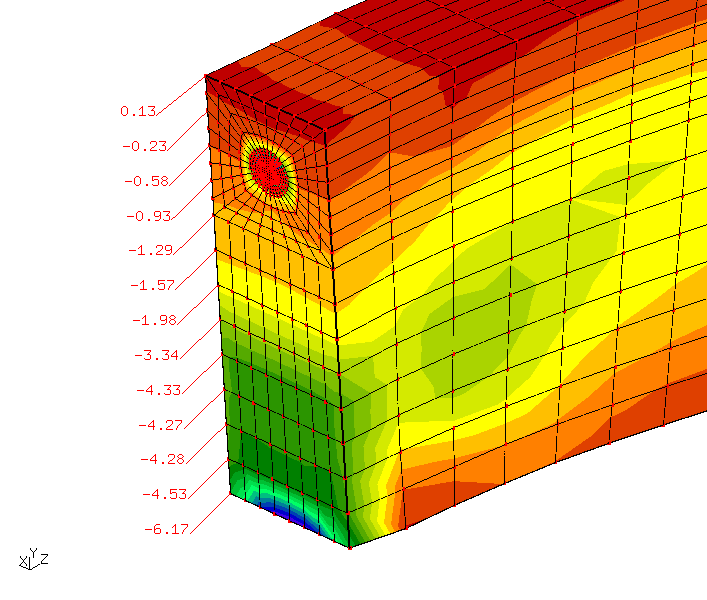
terlihat nilai kohesi erat hubungannya dengan batasan tarik Rankine atau "tension cut-off" yg mana nilai tersebut adalah batasan maksimum tegangan tarik yg diperbolehkan terjadi. berdasarkan rujukan Eurocode nilai cohesi beton cukup kecil yaitu hanya 0.55 Nmm^2 untuk beton mutu f'c 30MPa dan pada Abaqus CAE menjadikan masalah stabilitas numerik seperti yg disampaikan oleh Chiruta G. (2014) dgn supervisor prof. J. Clausen (2015) bahkan pada analisa sejenis hanya digunakan nilai kohesi sebesar 7.5N/mm^2 dan ini jauh lebih besar dari yg sya gunakan hanya 3.0N/mm^2 pada CalculiX.
sya sudah mencobanya di CalculiX dengan parameter nilai kohesi tersebut serta penggunaan sudut geser friksi sebesar 9deg rekomendasi dari Eurocode, konvergensi solver cukup lama dan belum sampai selesai.. nanti saya coba lagi.
***updates
menggunakan nilai kohesi (c=1.5Nmm^2) mendekati nilai yg direkomendasikan oleh Montoya (1971) yg diambil dari paper Ardiaca (2009), nilai sudut geser friksi dan dilatansi dibuat tetap.

running cukup lama dan solver tidak mencapai konvergensi, hanya sekitar 81% tahap beban diterapkan. artinya hasil tidak dapat digunakan, namun sebagai gambaran saja sebagai perbandingan dgn sebelumnya.

defleksi pada step ~81%
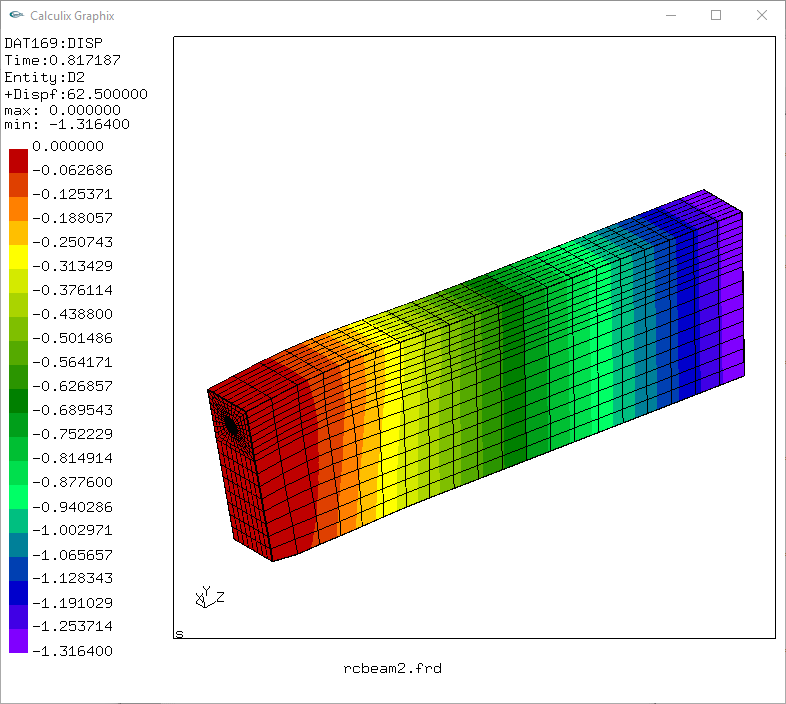
tegangan lentur,

tegangan geser,

kegagalan solver tersebut yg tidak mencapai konvergensi perlu dicari penyebabnya (?) dan ini ada kemungkinan dari penerapan beban sya yg terlalu tinggi, diperkirakan sudah gagal karena berkisar 3x lipat kapasitas geser balok.
sebagai informasi tambahan mengenai rekomendasi nilai kohesi untuk beton dari :

jadi penggunaan nilai yg digunakan terakhir sebesar 3.0 N/mm^2 pada data masukan analisa cukup reliable untuk kepemilikan beton pada umumnya.
sedangkan untuk nilai sudut geser friksi atau sudut friksi dalam (internal angle friction) hasil penelitian Suenaga (1998) untuk beton normal (Fc~26.5Nmm^2) menunjukan nilainya berkisar antara 37 - 55 deg dan nilai maksimum tsb mendekati dgn nilai sesuai Wegde Theory.

biasanya analisa model dgn material beton menggunakan kriteria Drucker-Prager namun pada CalculiX belum diimplementasikan UMAT tersebut. terlihat dari rujukan grafik diatas, penggunaan nilai sudut geser friksi yang kecil akan menjadikan bentuk kurva modifikasi Mohr-Coulomb mendekati kurva Drucker-Prager.

criteria for Modified MC materials (source: Clausen etal, 2006)
berbeda dgn program FE nonlinear, umumnya yg diutamakan adalah perilaku nonlinear materialnya. untuk material yg dominasi kemampuannya tekan dan getas maka akan banyak pilihan pada program advanced FE seperti adanya jenis nonlinear material Mohr Coulomb atau Drucker Prager yg biasa diaplikasikan untuk pemodelan pondasi atau dinding penahan tanah dan pemodelan beton bertulang. jenis material elasto-plastis yg lebih sederhana dari kedua material elasto-plastis diatas adalah Compression_Only material yg sudah tersedia pada program elemen hingga CalculiX versi 2.8 keatas.

perbandingan kurva diatas dengan material beton hasil pengujian tegangan biaxial dari Kupfer (1973) yg sya ambil dari paper Como etal (2007) ada sedikit perbedaan dimana pada tegangan tekan biaxial maka kemampuannya akan meningkat sampai sekitar 25% dari kondisi tegangan uniaxial.

disini saya mencoba meninjau secara singkat dan belum sampai ke perbandingan pendekatan secara teoritis, contoh adalah balok beton bertulang (bxh=20x40cm) kantilever (l=2.0m) dengan beban merata pada permukaan atas. mutu tekan beton (fc=30MPa) kapasitas tegangan tarik material ditentukan sebesar 10% dari kapasitas tegangan tekan umumnya. mutu tekan beton tsb dalam hal ini hanya sebagai acuan tidak berpengaruh pada analisa dgn elemen hingga menggunakan material Compression_Only.

tulangan dimodelkan dengan elemen truss (T3D2) mengunakan material yg masih elastis, hubungan dengan node elemen solid beton dianggap monolit sempurna.

deformasi,


tegangan lentur,


tegangan geser,

walau belum dilakukan validasi atau verifikasi namun sekilas hasil dan perilaku menunjukkan seperti yg diperkirakan. tegangan tarik sebagian besar diterima oleh tulangan atas, sedangkan tegangan geser hanya diterima pada balok yg mengalami tekan (tidak retak). masih ada beberapa yg belum sesuai, diantaranya adalah sisi tumpuan bagia atas yg mengalami tarik seharusnya sudah retak dan kemudian tegangan tarik diterima penuh oleh tulangan.
dibawah dicoba dengan mengabaikannya kapasitas tarik material pada elemen solid balok beton, ditentukan nilai hanya sebesar 1% kuat tekannya. dan hasilnya menunjukan sebagai berikut,

terlihat saat mengabaikan kemampuan tarik material beton menjadikan tegangan tarik baja tulangan atas dan tegangan tekan balok beton sisi bawah meningkat cukup signifikan.
*updates
model balok diatas menggunakan material beton elasto-plastis kriteria Modified Mohr Coulomb (Abaqus UMAT by J. Clausen, 2006)
defleksi,

tegangan lentur,


tegangan geser,


perlu model yg lebih realistis yaitu representasi tulangan dengan elemen solid, ditambahkannya pengaruh tahanan geser dan kekangan dari tulangan sengkang. juga pelu diterapkan nonlinearitas materil baja tulangan tersebut. lainnya yg tidak boleh terlewat adalah perbandingan dengan analisa secara pendekatan teoritis perhitungan tangan sebagai acuan awal.
**updates
model diatas agak rumit terutama saat pemodelan tulangan sengkang, sya coba model yg lebih sederhana untuk mencari perkiraan awal perbedaan pemodelan tulangan pokok dengen elemen truss (t3D2) dan full solid. ditinjau balok 50x150mm panjang 500mm. material hanya tekan (kapasitas 10%), beban merata.
lendutan,

tegangan lentur,


tegangan geser,


terlihat hasilnya mendekati, dapat diartikan model tulangan pokok dgn elemen truss (T3D2) dapat digunakan untuk memprediksikan awal. perbaikan model tetap diperlukan seperti model tulangan dgn elemen solid, diikut sertakannya model tulangan sengkang dan kriteria elasto-plastis materialnya.
***updates
model balok beton bertulang sederhana diatas menggunakan material elasto-plastis kriteria Modified Mohr Coulomb (Abaqus UMAT by J. Clausen, 2006)

defleksi,

tegangan lentur,


tegangan geser,


tegangan tarik pada balok beton yg terjadi pada sisi atas masih cukup besar, ini kemungkinan besar disebabkan dari penentuan nilai parameter dari material modified MC yaitu angle of internal friction, dilatancy dan cohesion. perlu dicari rujukan dalam penentuan nilai tersebut hubungannya dengan mutu tekan beton (?)

source: Ardiaca, 2009
menggunanakan parameter nilai kohesi (c=3.0 N/mm^2) sedangkan nilai lainnya tetap.
lendutan,

tegangan lentur,

penekanan tampilan warna batas/kontur sisi bawah - tegangan tekan,

penekanan tampilan warna batas/kontur sisi atas - tegangan tarik,

tegangan geser,


terlihat nilai kohesi erat hubungannya dengan batasan tarik Rankine atau "tension cut-off" yg mana nilai tersebut adalah batasan maksimum tegangan tarik yg diperbolehkan terjadi. berdasarkan rujukan Eurocode nilai cohesi beton cukup kecil yaitu hanya 0.55 Nmm^2 untuk beton mutu f'c 30MPa dan pada Abaqus CAE menjadikan masalah stabilitas numerik seperti yg disampaikan oleh Chiruta G. (2014) dgn supervisor prof. J. Clausen (2015) bahkan pada analisa sejenis hanya digunakan nilai kohesi sebesar 7.5N/mm^2 dan ini jauh lebih besar dari yg sya gunakan hanya 3.0N/mm^2 pada CalculiX.
sya sudah mencobanya di CalculiX dengan parameter nilai kohesi tersebut serta penggunaan sudut geser friksi sebesar 9deg rekomendasi dari Eurocode, konvergensi solver cukup lama dan belum sampai selesai.. nanti saya coba lagi.
***updates
menggunakan nilai kohesi (c=1.5Nmm^2) mendekati nilai yg direkomendasikan oleh Montoya (1971) yg diambil dari paper Ardiaca (2009), nilai sudut geser friksi dan dilatansi dibuat tetap.

running cukup lama dan solver tidak mencapai konvergensi, hanya sekitar 81% tahap beban diterapkan. artinya hasil tidak dapat digunakan, namun sebagai gambaran saja sebagai perbandingan dgn sebelumnya.

defleksi pada step ~81%

tegangan lentur,

tegangan geser,

kegagalan solver tersebut yg tidak mencapai konvergensi perlu dicari penyebabnya (?) dan ini ada kemungkinan dari penerapan beban sya yg terlalu tinggi, diperkirakan sudah gagal karena berkisar 3x lipat kapasitas geser balok.
sebagai informasi tambahan mengenai rekomendasi nilai kohesi untuk beton dari :
- CEB-FIB Model Code (2010) menerangkan nilai tersebut diantara 1.5 - 3.5 N/mm^2
- Mattock (1974) menerangkan nilai tersebut berkisar 2.8 N/mm^2
- AASHTO LRFD (2007) dapat diambil dari hasil uji geser langsung, tau_v = c * A_cv
- Vecchio etal (2001) dapat diambil dgn rumusan hubungan dgn sudut geser friksi,

jadi penggunaan nilai yg digunakan terakhir sebesar 3.0 N/mm^2 pada data masukan analisa cukup reliable untuk kepemilikan beton pada umumnya.
sedangkan untuk nilai sudut geser friksi atau sudut friksi dalam (internal angle friction) hasil penelitian Suenaga (1998) untuk beton normal (Fc~26.5Nmm^2) menunjukan nilainya berkisar antara 37 - 55 deg dan nilai maksimum tsb mendekati dgn nilai sesuai Wegde Theory.

source: DIANA FEA (2010)
biasanya analisa model dgn material beton menggunakan kriteria Drucker-Prager namun pada CalculiX belum diimplementasikan UMAT tersebut. terlihat dari rujukan grafik diatas, penggunaan nilai sudut geser friksi yang kecil akan menjadikan bentuk kurva modifikasi Mohr-Coulomb mendekati kurva Drucker-Prager.