[draft]
dalam analisa struktur gedung terhadap beban gempa biasanya digunakan asumsi lantai yang sangat kaku tak terhingga sehingga distribusi beban yg diterima tiap kolom sebanding dengan kekauan dan jarak terhadap pusat massa. dalam banyak hal terlihat ini sudah memenuhi, namun untuk keadaan tertentu tidak, diantaranya adalah pada struktur dengan diqfragma yang panjang, sedangkan pada jenis struktur laian adalah atap baja.

(source: Elwood, 2011)
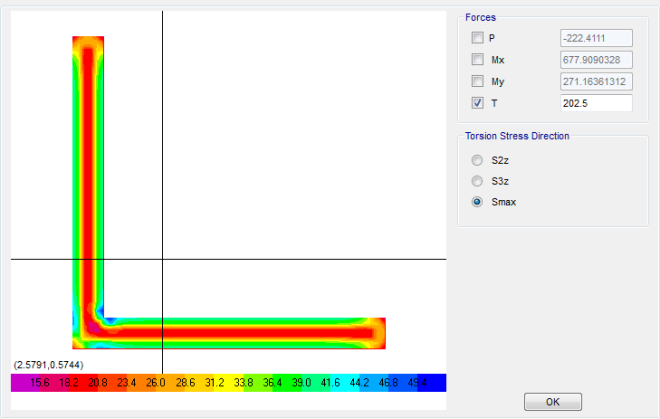
Saat beban gempa bekerja lantai diafraghma akan mengalami tegangan tarik, tekan dan geser sesuai kekauan dan distribusi massa (line/areas). Tegangan akan cukup berpengaruh jika terdapat kekakuan lateral kolom yg selisih besar dibanding lainnya seperti adanya dinding geser (shear wall). Secara analisa diafragma dapat ditinjau sebagai elemen tegangan bidang (plane stress) dengan ditumpu oleh kekakuan pegas tranversal kolom dan dinding geser, beban yg dikerjakan adalah distributed area loads untuk massa lantai, line loads untuk massa dinding dan concentrated load untuk massa terpusat jika ada. apada kasus sederhana dengan massa yg bekerja hanya uniform dari lantai dan kekauan tranversal yg ditinjau hanya diterima dinding geser ini dapat digunakan metode analisa balok biasa untuk difragma panjang/slender atau metode strut & tie (STM) untuk bentang pendek. analisa diafrgma dgn metode elemen hingga (FEM) dgn menggunakan element plane stress dapat digunakan untuk kasus sembarang yg lebih luas dimana beban dari massa dan reaksi dapat dimodelkan secara aktual keseluruhan.

fig. tegangan pada lantai diafragma
Dalam analisa lantai diafragma, seharusnya kekakuan balok diabaikan sehingga tegangan hanya diterima oleh pelat diafragma. hal ini ditujukan untuk menjaga konsistensi perhitungan pada desain balok itu sendiri karena hanya didesian menerima lentur/geser sumbu major serta torsi(jika ada). prosedur desain balok tidak dapat digunakan dan akan menjadi rumit jika elemen menerima gaya tarik, untuk gaya tekan masih memungkinkan diabaikan jika P<0.1*f'c*Ag. hasil analisa lantai diafrgma dengan FEM yg terutama ditinjau adalah terhadap tegangan tarik, yg mana ini akan membutuhkan penulangan khusus tension chord diapraghm. sedangkan lainnya adalah tegangan tekan dan geser yg mana ini biasanya sudah memenuhi karena dimensi dari lebar diafraghma yg besar.

fig. pembesian khusus lantai diafragma
(souce: Moehle etal, 2010)
Perbedaan dari asumsi lantai difragma diatas adalah terletak pada distribusi beban yg diterima tiap portal kolom lantai. pada asumsi lantai tidak kaku (flexible) distribusi beban gempa tidak dipengaruhi perbedaan kekauan tranversalnya, beban gempa hanya didasarkan batasan luasan beban setengah jarak sebelahnya (tributary areas). beban lateral tambahan akibat torsi tidak ada pada asumsi flexible ini.

fig. distribusi beban gempa pada lantai dgn asumsi flexible diapraghm
Pada analisa dengan asumsi lantai diafragma yg kaku (rigid) dengan eksentrisitas nul dan kekakuan kolom seragam distribusi beban gempa akan diterima sama tidap titik baik itu kolom dalam, luar atau tepi. sedangkan pada samusi diantaranya yaitu semi rigid menggunakan kekakuan aktual dari lantai diafragma, distribusi beban gempa sesuai dengan konfigurasi lantai dan kekakuan kolom dan/atau dinding geser penahan tranversalnya. akan ada beban lateral tambahan yg diterima kolom akibat puntir eksentrisitas pusat masa dengan pusat kekakuan pada konfigurasi lantai suatu gedung irregular.

fig. kategori kekauan lantaii diafragma (source: ASCE, 2005)

fig. kategori regularitas suatu lantai bangunan (souce: FEMA, 2006)
Berikut adalah contoh sederhana kondisi bangunan irregular akibat perbedaan distribusi massa dan kekakuan penahan lateralnya,

3D extruded view


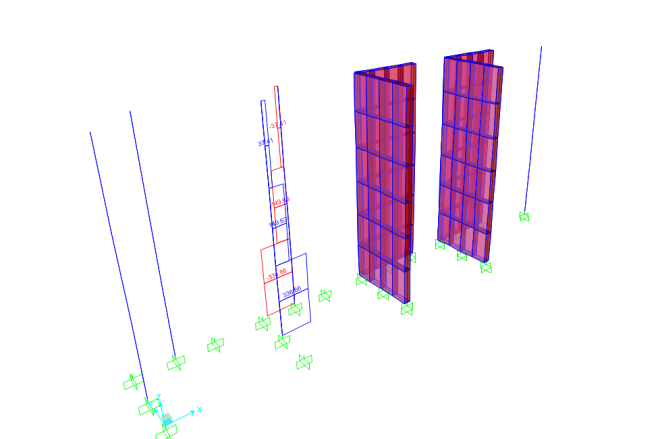
Beban lantai (kN-m units)

Beban Dinding (kN-m units)



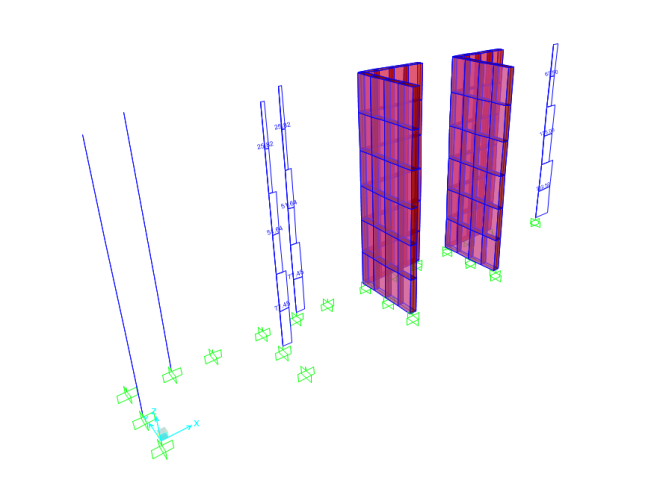
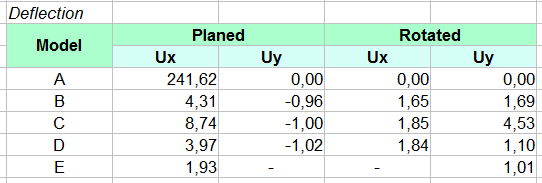
Deformasi akibat unit loads untuk mecari kooindiat pusat kekakuan (Center of Rigidity)

Perhitungan koodinat pusat massa (Center of Mass) dan pusat kekakuan (Center of Rigidity) serta kategori regularitas lantai bangunan.

eksentrisitas anatar pusat massa dan pusat kekakuan
Model struktur dengan kekauan lantai diafragma aktual, tinjuan gempa arah-Y sebesar 0.2g,

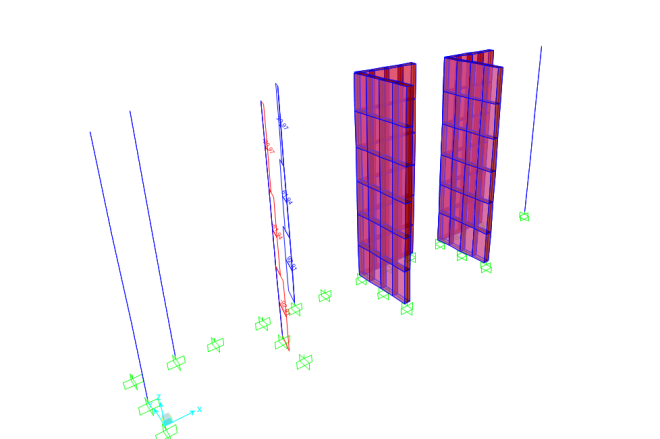
beban gempa dari lantai

beban gempa dari dinding

defleksi arah-X

defleksi arah-X

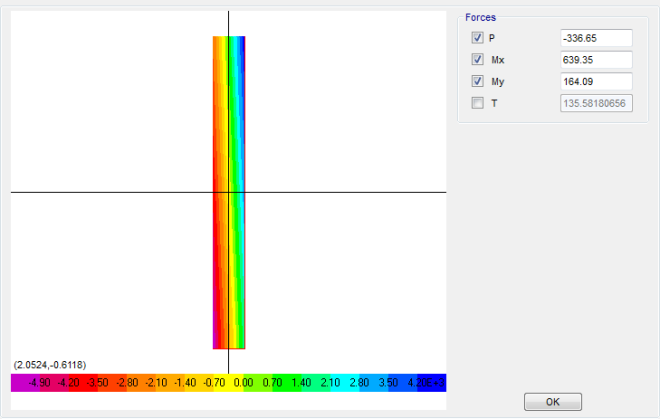
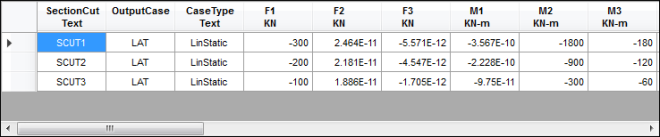
Gaya Aksial (Axial Force)


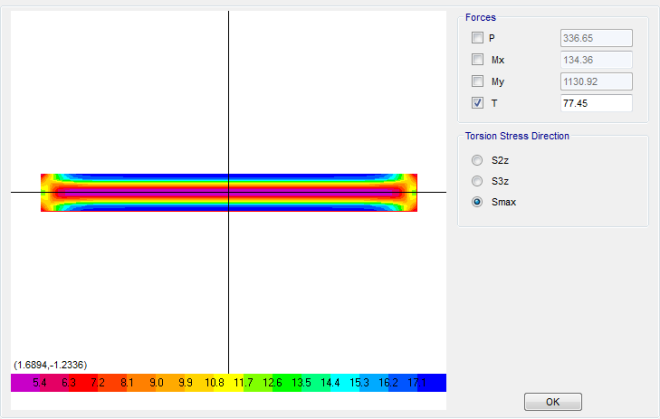
Gaya Geser (Shear Force)


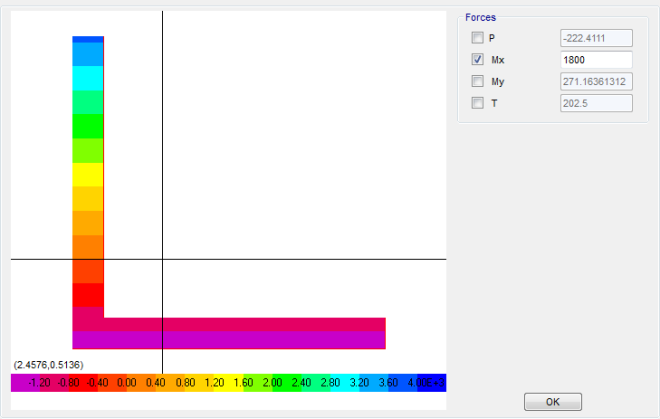
Gaya Lentur (Bending Moment)

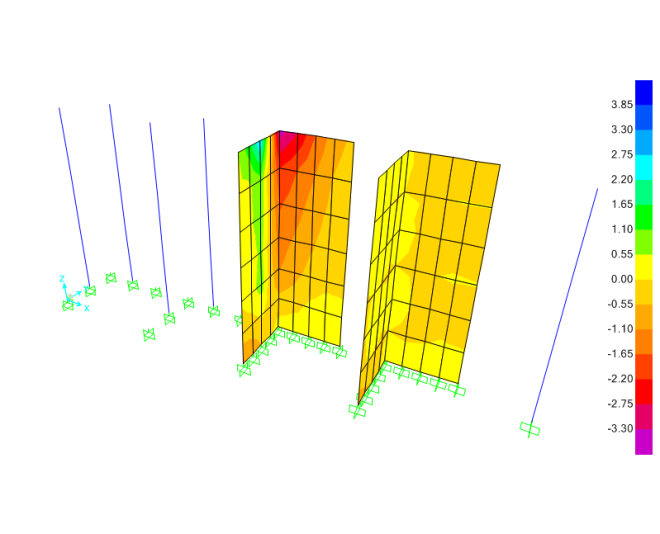
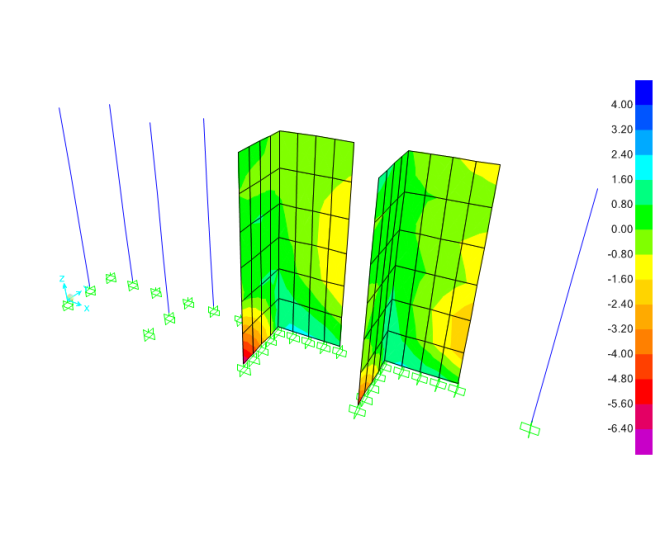
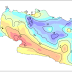
Tegangan lantai diafrgma S11 (N/mm2)

Tegangan lantai diafrgma S22 (N/mm2)
Dalam hal diatas tegangan yg terjadi cukup kecil sehingga kelihatannya tidak memerlukan tulangan khusus, pembesian minimum pelat bagian bawah pada tumpuan negatif mungkn sudah mencukupi (?)
to be added,
- hand calculation, terhadap tension chord, compression & shear lantai diafragma.
- hand calculation, center of rigidity & center of mass. untuk C.o.R asumsi shear building dgn kekauan balok infinity
- example case with known solution from reference, further comparison with FEM results
- lantai bangunan dengan large void