estimasi tulangan perlu balok beda tinggi

Tulisan ini melanjutkan sebelumnya, mengenai balok tinggi dengan perbedaan dimensi tinggi penampang. Konsentrasi tegangan di sudut patahan pertemuan penampang membuat retakan diagonal, mengenai sudut dan pola retak tergantung dari konfigurasi tulangan yang ditentukan. Program advanded FE yang sudah memasukkan pengaruh nonlinearitas seperti ANSYS/ABAQUS dan ATENA/MERLIN atau lainnya dapat memprediksikan pola retak dan beban ultimit, sedangkan STM hanya pada kapasitas saja dgn nilai batas bawah.

(source: Wang et al, 2005)

Pemodelan STM balok tinggi dgn perbedaan dimensi tinggi, analisa  dan hasil konfigurasi pembesian merujuk pada pustaka El-Metwally et al (2011)





Berikut tampilan model, hasil analis dan perbandingan estimasi kebutuhan tulangan,

Geometri, beban dan kondisi tumpuan

Tegangan prinsipal beton (tebal elemen tidak diperhitungkan penuh)

Alur tegangan utama (warna magenta adalah tekan & warna biru untuk tarik)

Kebutuhan tulangan perlu arah datar (H)

Keutuhan tulangan perlu arah tegak (V)

Grafik perbedaan hasil ditampilkan dgn bar chart berikut,

Terlihat berbeda untuk jenis balok tinggi ini, terutama daerah sudut patahan dimana hasil Elastic FE mendistribusikan pada kedua sisi (atas/bawah, kiri/kanan) sedangkan STM terkonsentrasi salah satu sisi saja. Konsep kedua metode tersebut memang berbeda, sehingga konfigurasi tulangan juga akan berbeda. Perlu pembanding lanjut dengan program nonlinear FE sebagai virtual labs tujuan untuk dasar simulasi model.

calculation pads,

' Ties (T1)
As1a=Avg(12.019,8.585,6.901,6.073,5.246,4.184,3.286,2.352,1.297,0.675)*(2333-1500)*0.9/0.75*2= 10119.55mm2
As1b=Avg(4.911,4.700,4.290,3.685,2.460,1.647,0.833)*(2333-1500)*0.9/0.75*2= 6433.43mm2
' reffs
T1 = 2095kN
Asr = (T1*10^3)/(0.75*460)= 6072.46mm2
Asp = 16*(1/4)*Pi*22^2= 6082.12mm2
' Ties (T2)
As2a=Avg(9.458,6.829,4.283,3.667,2.655,2.259,1.768,1.414,1.107,0.777,0.923,0.604,0.468)*(6250-5615)*0.9/0.75*2= 4245.16mm2
As2b=Avg(9.458,5.706,1.955,0.384,0.337,0.190,0.086)*(6693-6250)*0.9/0.75*2= 2751.56mm2
' reffs
T2 = 1091kN
Asr = (T2*10^3)/(0.75*460)= 3162.32mm2
Asp = 2*14*(1/4)*Pi*12^2= 3166.73mm2
' Ties (T3)
As1a=Avg(1.067,3.165,2.488,1.599,1.518,1.436,1.144,0.851)*(750-0)*0.9/0.75*2= 2985.30mm2
As1b=Avg(1.516,1.439,1.380,1.322,1.265,1.160,1.055,0.975,0.896)*(750-0)*0.9/0.75*2= 2201.60mm2
As1c=Avg(12.019,7.343,0.4289,0.314,0.200,0.139,0.0786,0.0628,0.047)*(1500-750)*0.9/0.75*2= 4126.46mm2
' reffs
T3 = 1091kN
Asr = (T3*10^3)/(0.75*460)= 3162.32mm2
Asp = 10*(1/4)*Pi*20^2= 3141.59mm2

Read More

melihat rujukan kuat geser balok beton tanpa begel

Parameter yang mempengaruhi kuat geser balok beton tanpa begel diantaranya adalah dimensi:lebar & tinggi effektif, mutu beton (f'c),  perbandingan jarak titik geser terhadap tinggi effektif, perbandingan nilai geser ultimit (Vu) dan momen ultimit (Mu).
[scribd id=63218770 key=key-2ne6x387evayattdn8n mode=list]

Berikut plot grafik bar chart kuat geser balok tanpa begel dari beberapa rujukan,



Selanjutnya dilakukan perbandingan dgn program analisa penampang beton dengan model tanpa begel dan dipasang begel minimum. Terlihat hasilnya yaitu (90.7kN dan 102.8kN) sedikit lebih kecil atau mendekati dibandingkan kebanyakan rujukan.

Dimensi, mutu baja & beton serta tulangan terpasang.

Balok beton tanpa begel

Balok beton dgn begel dibawah minimum

Read More

estimasi tulangan perlu balok tinggi jenis corbel

Tulisan ini melanjutkan sebelumnya, mengenai balok tinggi jenis corbel. Rujukan pustaka dari Singh etal (2005), pembebanan dan geometri simetris sehingga hanya dimodelkan separuh untuk mereduksi DOF's dan waktu penyelesaian.

Loads, Geometry and STM models (source: Singh etal, 2005)

Elastic Linear FE models & results



 

fig.2



fig.3



 

 

fig.4

Reinforce bars arrangement

(source: Singh etal, 2005)

Kontur kebutuhan tulangan perlu hasil SAP

Arah datar (H)

Arah Tegak (V)

Calculation pads,

' Horizontal
As1=Avg(8.661,3.861,2.449,1.464,1.158)*(750-627)*0.9/0.75*2 = 1038.69 mm2
' Reffs
Asr = (284.68*10^3)/(0.75*415) = 914.63 mm2
Asp = 6*0.25*Pi*16^2 = 1206.37 mm2
' Vertical
As2=Avg(1.307,1.296,0.656,1.259,0.527)*(300-250)*0.9/0.75*2 = 121.08mm2
' Reffs
Asmin=283.3 mm2

Read More

estimasi tulangan perlu balok tinggi berlubang

Tulisan ini melanjutkan sebelumnya, mengenai hasil pembesian tulangan balok tinggi dengan elastic FE program bantu SAP. Keadaan lain yang ditinjau adalah pengaruh adanya lubang.

Elastic FE models

Stress path

Concrete principal stress

Elastic Linear FE

Nonlinear FE (Muttoni etal, 2007)

STM models

(source: Muttoni etal, 2007)

fig.3

(source: Steven etal, 2000)

Reinforce bars arrangement

fig.4

fig.5

Kontur tulangan perlu arah datar (H)

Kontur tulangan perlu arah tegak (V)

Perbedaan hasil ditampilkan dengan bar chart berikut,



Pola retak dan kapasitas beban ultimit pada beberapa jenis model STM dan konfigurasi tulangan hasil penelitian Maxwell, B.S. (1996) dgn scaled down 5.5



Terlihat konfigurasi tulangan orthogonal dgn kombinasi diagonal menghasilkan kapasitas beban ultimit lebih besar dibandingkan konfigurasi tulangan lainnya. Semua model mencapai beban terfaktor yg direncanakan sebesar 22Kips (Maxwell, 1996)

 

calculation pads,

' Horizontal bars Reinforcement
As1=Avg(3.599,1.735,0.719,0,0)*500*0.9/0.75= 726.36
reff1a=2*0.25*Pi*25^2= 981.75
reff1b=2*0.25*Pi*20^2= 628.32
As2=Avg(2.558,0.702,1.267,1.124,0.878)*500*0.9/0.75= 783.48
reff2a=2*0.25*Pi*25^2= 981.75
reff2b=3*0.25*Pi*20^2= 942.48
As3=Avg(3.833,2.095,1.359)*(2338-2000)*0.9/0.75= 985.20
reff3a=2*0.25*Pi*25^2= 981.75
As3=Avg(3.833,2.095,1.359,0.698)*(2675-2000)*0.9/0.75= 1616.96
reff3b=7*0.25*Pi*16^2= 1407.43
As4=Avg(2.775,0.0386,0.0481,0.031,0.005,0.073,0)*(2000-500)*0.9/0.75= 763.89
reff4=6*0.25*Pi*12^2= 678.58
As5=Avg(3.832,0.553,0.153,0.102,0,0.143,0)*(2000-500)*0.9/0.75= 1229.91
reff5=6*0.25*Pi*12^2= 678.58
' Vertical bars Reinforcement
As1=Avg(3.343,1.716,1.165,0.700)*(2625-2000)*0.9/0.75= 1298.25
reff1a=2*0.25*Pi*25^2+2*0.25*Pi*12^2= 1207.94
As1=Avg(3.343,1.716,1.165,0.700,0.456)*(2938-2000)*0.9/0.75= 1661.39
reff1b=7*0.25*Pi*16^2= 1407.43
As2=Avg(0,0.640,0.097,0.153,0.148,0.571,3.343)*(2000-500)*0.9/0.75= 1273.37
reff2a=7*0.25*Pi*12^2= 791.68
reff2b=6*0.25*Pi*12^2= 678.58
As3=Avg(0.049,0.021,0.027,0.025,0.029,0.027,0.027,0.0258,0.027,0.022,0.029,0.018,0.04,0.027,0.06,0.071,0.121,0.258,0.492,2.6180)*(7000-2000)*0.9/0.75= 1204.14
reff3a=16*0.25*Pi*12^2= 1809.56
reff3b= 0.00
' Minimum bars reinforcement
A_smin=0.002*1000*400-50= 750.00

Read More

kontribusi kekakuan balok sekunder

Tulisan ini merupakan kelanjutan dari sebelumnya, mengenai distribusi beban dua arah pada struktur beton bertulang dimana saat ini ditinjau pengaruh balok sekunder/pembagi yang biasa ditemui pada bangunan lokal.

The actual distribution of loads on these elements is quite complex. ETABS uses the concept of tributary loads as a simplifying assumption for transforming the loads (CSi,1999)

I took simple frame models to check, it contains secondary beams with different stiffness near to 4 times lower compared to main beams.



Figures above shows extruded 3d views, left models with automatic area loads to frame done by SAP another using finite element models with considering beam to slab eccentricity.



Bending moment diagrams, right models has low values.



Zero axial force in beams for left models, contrary high axial force (tension) exist in right models due to eccentricity modeling with rigid links.



Slab act in compression by couple tension force in beams, it may be figuring as tee-beam with flanges effective width.

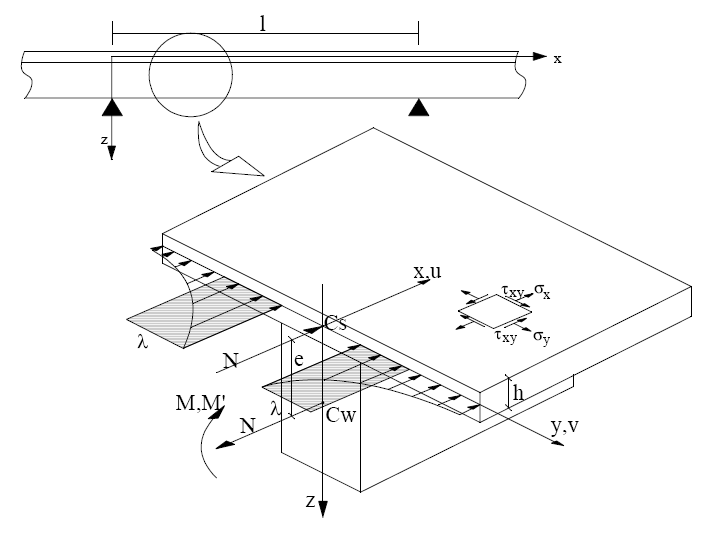(source: Chiewanichakorn, etal. 2001)

Using tributary areas load concept will ignore variable stiffness of beams  in a panel being considered. FE models do betters in prediction but required  additional nodes and computational effort. In case slab panel  with secondary beams, bending moment will varies depending geometry and beams sectional properties. Another approach is remove secondary beams with equivalent slab stiffness with modified flexural rigidities of plates may required for this cases to avoid unacceptable results and it's behavior.

Calculation pads,

' Tributary area concept
' Beam-Y
' B30/60
M_1 = 69.7;
' B30/40
M_2 = 69.56;
' Beam-X
' B30/60
M =116.49;
' FE approximation
' Beam-Y
' B30/60
M_e=40.59
M_a=177.06*0.24= 42.49
M=M_e+M_a= 83.08 kN.m
' B30/40
M_e=32.32
M_a=168.63*0.14= 23.61
M=M_e+M_a= 55.93 kN.m
' Beam-X
' B30/60
M_e=67.93
M_a=214.46*0.24 = 51.47
M=M_e+M_a = 119.40 kN.m
' Flexural Reinforcement (hand calculations)
' Tributary approximation
' Beam-Y
' A_s1 < A_smin = 590.10 mm2 (B30/60)
' A_s2 = 634.89 mm2 (B30/40)
' Beam-X
' A_s = 672.62 mm2
' FE approximation
' Beam-Y
' A_s1 < A_smin = 590.10 mm2 (B30/60)
' A_s2 = 502.10 mm2 (B30/40)
' Beam-X
' A_s = 690.11 mm2 (B30/60)
'
' Beam Stiffness Ratio (middle & edge)
E_c=(4700*Sqrt(25))*10.19716= 239633.26 kgf/cm2
L = 600 cm
b1 = 30 cm
h1 = 60 cm
Ix1=1/12*b1*h1^3= 540000.00 cm4
b2 = 30 cm
h2 = 40 cm
Ix2=1/12*b2*h2^3= 160000.00 cm4
K_db1 = (48*E_c*Ix1)/L= 10352156832.00
K_db2 = (48*E_c*Ix2)/L= 3067305728.00
R_db=K_db1/K_db2= 3.38 (~4 times stiffness)
' Beam internal moment ratio (secondary beams 30/40)
M_x1 = 69.56;
M_x2 = 55.93;
R_mx = M_x1/M_x2= 1.24 (~ 25%higher)

' Beam internal moment ratio (main beams 30/60)

M_x3 = 69.70;
M_x4 = 83.08;
R_mx = M_x3/M_x4= 0.84 (~15%lower)

Read More

penghalusan garis lengkung untuk visualisasi

pada program render seperti KT untuk model curve akan terlihat patah2 (segmental) jika modeling pada SkethUp menggunakan nilai default saat menggambar object lingkaran karena pendekatan yang dilakukan mengunakan polyline (segmental) dengan 24 garis penghubung.



untuk lengkung yang diharapkan halus perlu merubah setting menjadi setidaknya duakali lipat atau lebih, namun disis lain akan membutuhkan waktu lebih pada saat render nantinya.

Sesaat setelah menekan icon tombol circle atau keyword "C" lalu ketik 48 atau 96 untuk menentukan jumlah segment yang diinginkan, ini terletak dikanan bawah.



Hasil vertex dan face yang dihasilkan setelah diimport ke program render KT



Perbedaan tingkat kehalusan dapat dilihat setelah proses render selesai.

gambar visualisasi object beberapa koin perunggu

Read More

distribusi tegangan elastis berbagai tipe pondasi dangkal

(sumber: Esmaili D., etal - 2008)

Pondasi dangkal umumnya berbentuk tapak (footing/pad) dengan tujuan pekerjaan konstruksi menjadi mudah. Beberapa bentuk lain yg lebih effektif dibandingkan jenis tapak adalah jenis pondasi cangkang (shell) berbentuk seperti mangkuk terbalik yg tertanam, dapat berupa bulat atau pesegi.

Gbr.1 Pondasi Cangkang sebelum ditanam

Gbr. 2 Test pembebanan terukur (loading test)

Gbr.3 Grafik hasil pengukuran

(Sumber: Huat B.B.K., etal - 2007)

Pada tulisan ini akan dipelajari distribusi tegangan elastis dibawah pondasi dari beberapa jenis pondasi tersebut diatas. Analisa elemen hingga jenis plane strain menggunakan program bantu SAP. Walaupun jenis analisa masih elastis terlihat cukup dalam memprediksikan, namun akan lebih baik juga jika dilakukan dgn program bantu spesifik interaksi pondasi tanah yg advanced seperti PLAXIS sehingga dapat merepresentasikan interface dan nonlinearitas material tanah serta pola keruntuhan (failure surfaces).

Gbr. 4 Jaring elemen hingga (meshing FE)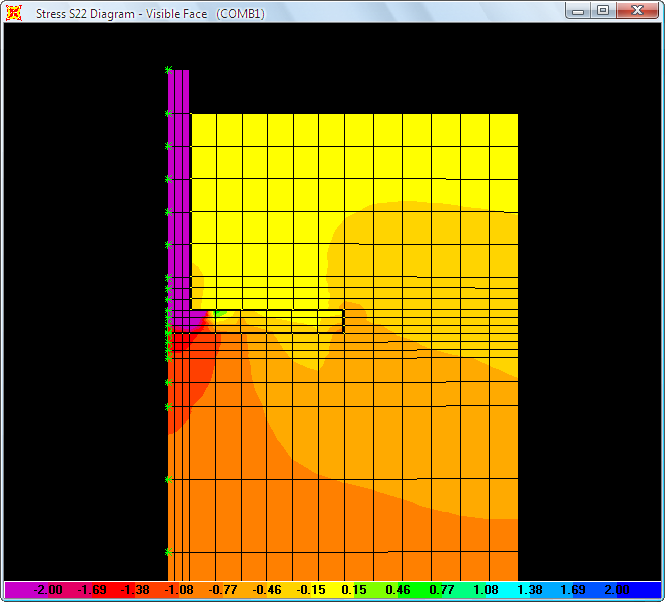

Gbr. 5 Distribusi tegangan jenis pondasi tapak

Gbr. 6 Distribusi tegangan jenis pondasi cangkang 1

Gbr. 7 Distribusi tegangan jenis pondasi cangkang 2

Terlihat jenis cangkang menunjukan distribusi tegangan tanah dan penurunan yg lebih rendah dibanding pondasi tapak biasa. Pada tegangan sendiri pelat pondasi juga memperlihatkan bahwa jenis cangkang menjadikan tegangan tekan beton (compression)  lebih merata yg berarti pembesian tarik akan minimum.

Banyak penelitian menunjukkan bahwa defleksi dari hasil analisa linear elastis FE biasanya lebih kecil dari sesungguhnya dgn selisih berkisar separuhnya, seperti diperlihatkan salah satu contoh grafik dibawah ini (Weber J.W., etall - 1984).

Read More