model struktur shell menggunakan dxf CAD

Pemodelan struktur shell yg bukan pesegi akan cukup rumit jika menggunakan GUI sap2000 cara lain yg cukup mudah adalah menggunakan fasilitas import DXF model dibuat dgn program AutoCAD atau IntelliCAD. Disini dijelaskan langkah-langkah pemodelannya, secara garis besar :

1. Pada program CAD, buat garis bantu face yg akan dibuat.


2. Partitioning dgn mengikuti element shell quadrilateral.


3. Generate surface tiap bagian dari struktur shell.


4. Buat layer baru dgn nama sembarang untuk object face yg dibuat.


5. Export gambar dgn pilihan DXF


6. 5.Pada program SAP2000, tentukan unit sesuai model awal serta pilih blank pada new model wizard.


7. Import file DXF dgn pilih nama layer yg ditentukan awal.


8. Setelah model berhasil di import dan tampil, select all lalu lkukan merge node dgn toleransi tertentu.


9. Test apakan sudah bekerja dgn baik, tentukan kondisi batas (tumpuan dan beban), material & shell element properties.


10. Run analysis, perhatikan deformasi dan kontur tegangan apakah sudah terlihat continue.

Dibawah ini gambar berikut catatan keterangannya.

Partisi dari lingkaran diameter D = 6.0m

Lakukan mirror dari 1/4 segment model partitioning lingkaran

Ulang untuk menyelesaikan pembuatan lingkaran penuh

ubah User Coordinat System, buat garis ketinggian H = 3.0m kemudian lakukan copy

Buat layer baru dgn nama "face" dapat aktif ditampilkan dan tidak

Generate surface dari empat garis tepi.

Rujukan pemodelan surface (ProgeCAD, 2008)

ulang untuk semua bagian partitioning struktur shell

Setting pias pembagi sisi satu dgn sisi lainnya

Tentukan satuan lalu pilih "blank" template

Menu file pilih import, lalu pilih AutoCAD .dxf File

Tentukan sumbu tegak pada DXF file yg telah ditentukan awal.

Pilih layer object Shell yg telah ditentukan saat pemodelan CAD

Done, object sudah berhasil di import dari DXF

Select All, lakukan merge nodes

Test model dgn penerapan kondisi batas (beban hidrostatis, tumpuan) dan properties (material&element), kemudian running.

Terlihat kontur momen sudah terlihat menerus tidak patah-patah yg berarti element quad shell sudah saling terhubung.

.

Dibawah juga diberikan contoh model lain, yg cukup beberapa step jika menggunakan CAD dan fasilitas import SAP2000.

.

.

.

.



.

Read More

balok portal pd beban layan tinjauan pesegi dan T

balok portal pd beban layan tinjauan pesegi dan T (in draft).

.

theoretical background

.



.



.



.

selisih momen lentur balok ~15%, sedangkan pada kolom ~25%

.

' Bentang balok portal
L = 9.00 m
b_eff1 = L/4 = 2.25 m
' Jarak antar balok
b = 3.50 m
b_eff2 = (b - 30cm) / 2 = 1.60 m
' Lebar balok
b_w = 30.00 cm
' Tebal slab
t_s = 10.00 cm
b_eff3 = b_w + 16*t_s = 1.90 m
' Dipilih terkecil
b_eff = Min(b_eff1,b_eff2,b_eff3) = 1.60 m
' Digunakan b_eff = 150 cm

.

Read More

pondasi lajur asumsi kaku tak terhingga dan tidak

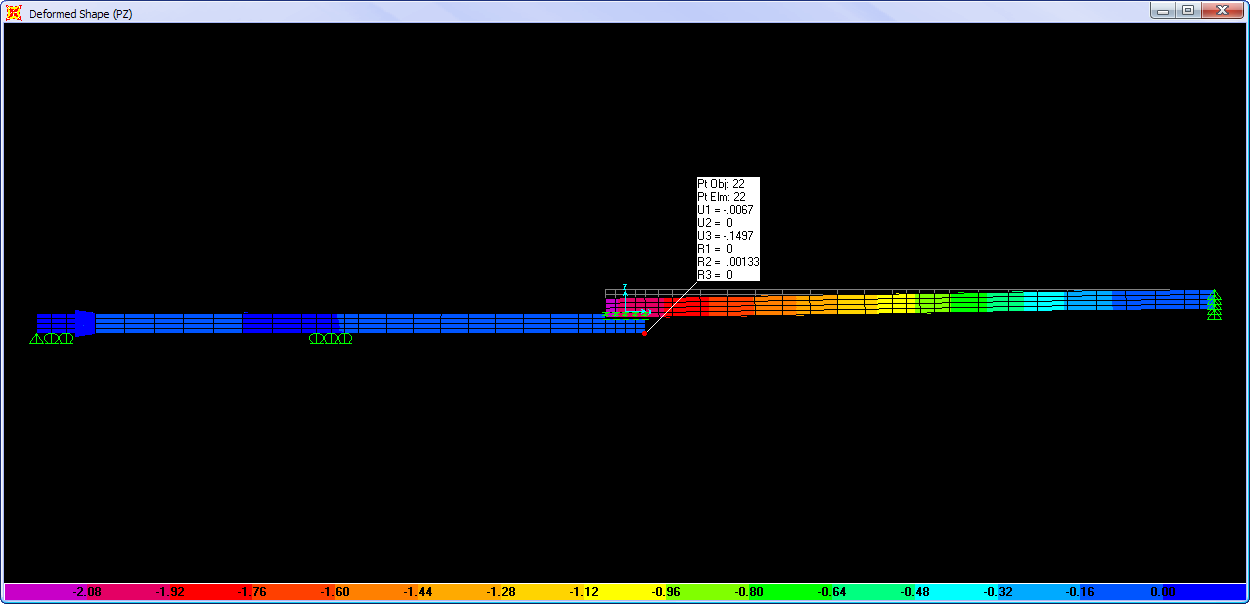
Tulisan ini dibuat saat ini ketika sdg review suatu bangunan perkantoran 3lt dgn sistem pondasi lajur atau menerus (continous footing). Tertarik karena jarang lihat, biasanya untuk bangunan seperti itu kisaran pancang jenis mini pile 4 sampai 6bh per titik kolom selain itu bangunan tersebut yg telah dbangun sekitar 20th yg lalu yg bisa dikategorikan sudah survive. Diperkirakan masih di desain dgn perhitungan tangan asumsi kekakuan pondasi dan/atau sloof tak terhingga (zero displacement) serta mengabaikan aksi dua arah.

" ... , a practicing engineer has no other option, but to perform hand calculations of any beam on Elastic Foundation as absolutely rigid , without taking into account the actual rigidity of the beam. While this method, in some cases, can be justified, it can also lead to serious mistakes." (Tsudik, 2006)

Analisa pondasi lajur atau setempat biasa dianalisa secara konvensional sebagai dasar yg kaku tak terhingga (absolutely rigid) berapapun panjang pondasi yg dipakai, kenyataannya tidak seperti itu. Asumsi sebagai pondasi kaku didasarkan pada penyederhanaan masalah analisa agar analisa dapat dilakukan dgn perhitungan kalkulator tangan.



Prinsip analisa pondasi rigid pada pondasi menerus adalah menjumlahkan semua gaya normal (P) dan momen (M) pada beberapa kolom yg ada, jika gaya aksi normal P berbeda tiap kolom maka akan di equivalensikan dgn eksentrisitas. Setelah itu ditinjau tegangan tanah yg terjadi akibat normal dan momen tersebut pengaruh luasan dan modulus penampang pondasi secara keseluruhan. Berbeda dengan mengunakan asumsi pondasi tumpuan elastis (winkler) gaya diterapkan langsung, tegangan tanah dihitung berdasarkan reaksi pegas dibagikan dengan luasan tributary area pegas itu sendiri.



Kekakuan pegas disebut sebagai modulus reaksi tanah dasar (modulus of subgrade reaction) ditentukan dari hubungan beban- penurunan hasil uji beban pelat (plate load test) luasan tertentu lalu dikonversikan dgn luasan pondasi sesungguhnya terpasang dgn merujuk pendekatan empiris rumus (Terzaghi,Vesic, Bowles, etc).  Jika tidak ada atau tidak memungkinkan dapat diambil pendekatan dari  rumus atau grafik tabel berbagai rujukan, bisa didasarkan jenis tanah dari N-SPT, DDT, atau nilai CBR. Ada yg agak sulit / tidak mudah dalam menentukan besaran kekakauan pegas (force/length) karena nilai ini pada suatu titik yg ditinjau akan lebih kaku yg besarnya sebanding tegangan tanah dasar atau reaksi pancang pd pondasi dalam gabungan.

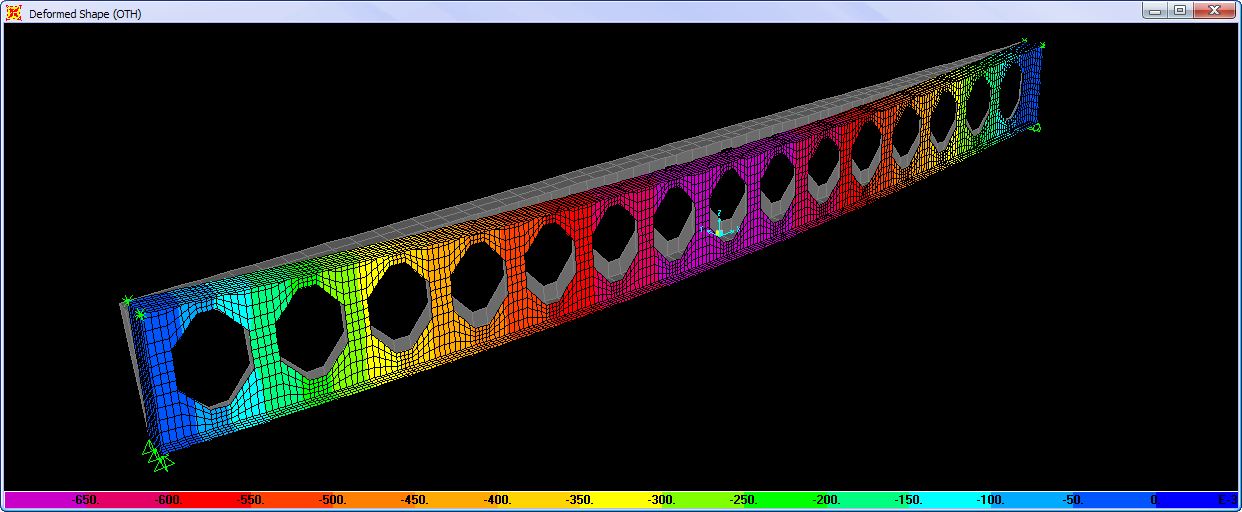
Berikut adalah contoh hasil keluaran dri program geoteknik yg advanced, kekakuan pegas Ks tidak diambil merata (uniform) melainkan didasarkan pada boring log di lapangan (E_soil, nu, Gamma, dll)  kemudian nilainya dilakukan iterasi terhadap pengaruh ketebalan dan properties tanah didasarnya serta beban yg bekerja pada suatu titik pondasi raft tsb. Pada contoh diatas perbedaan nilai pegas suatu titik dgn titik lainnya selisih berkisar 4~5 kalinya.



Diatas adalah keterangan beban titik, uniform dan lajur pada pondasi raft.

Plate load test (30inch dia)

Peraturan beton ACI merekomendasikan agar nilai tersebut dipakai berbagai tinjauan kondisi batas bawah dan batas atas, 1 (satu) sampai dengan 10 (sepuluh) kalinya, kemudian moment desain diambil yg menentukan (worst condition).



Analisa yg digunakan adalah balok diatas medium elastis, jika menggunakan software yg general purpose seperti SAP2000/SAFE mempunyai kekurangan karena pemodelan yg memungkinkan hanya model winkler sedangkan pemodelan lain yg advanced seperti Method of Initial Parameters, Elastic Half-Space atau Elastic Layer tidak bisa jadi perlu software khusus dan memang ini sudah lebih lanjut permasalahan geoteknik.



.



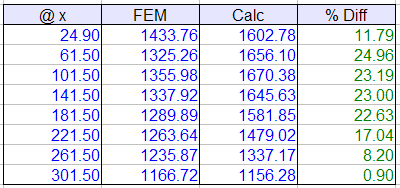
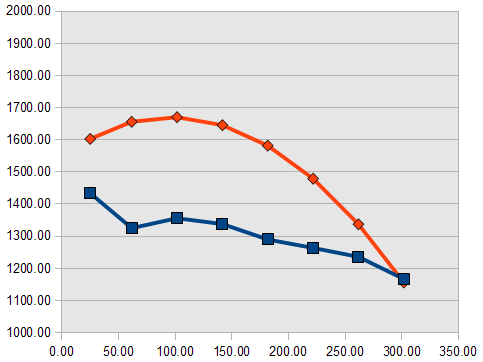
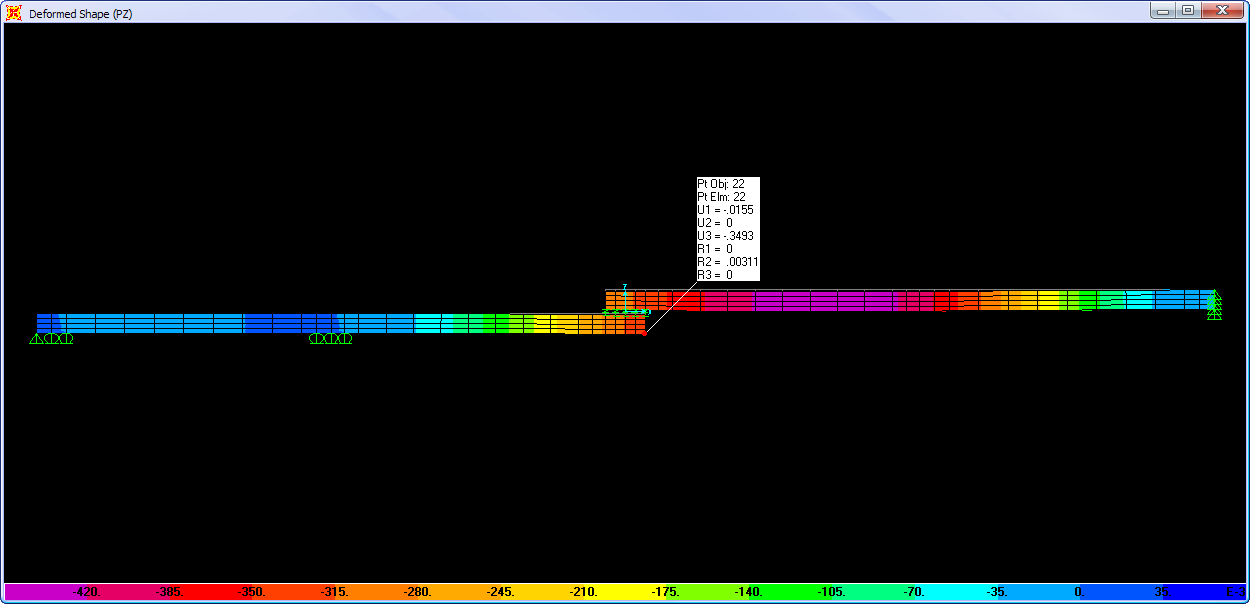
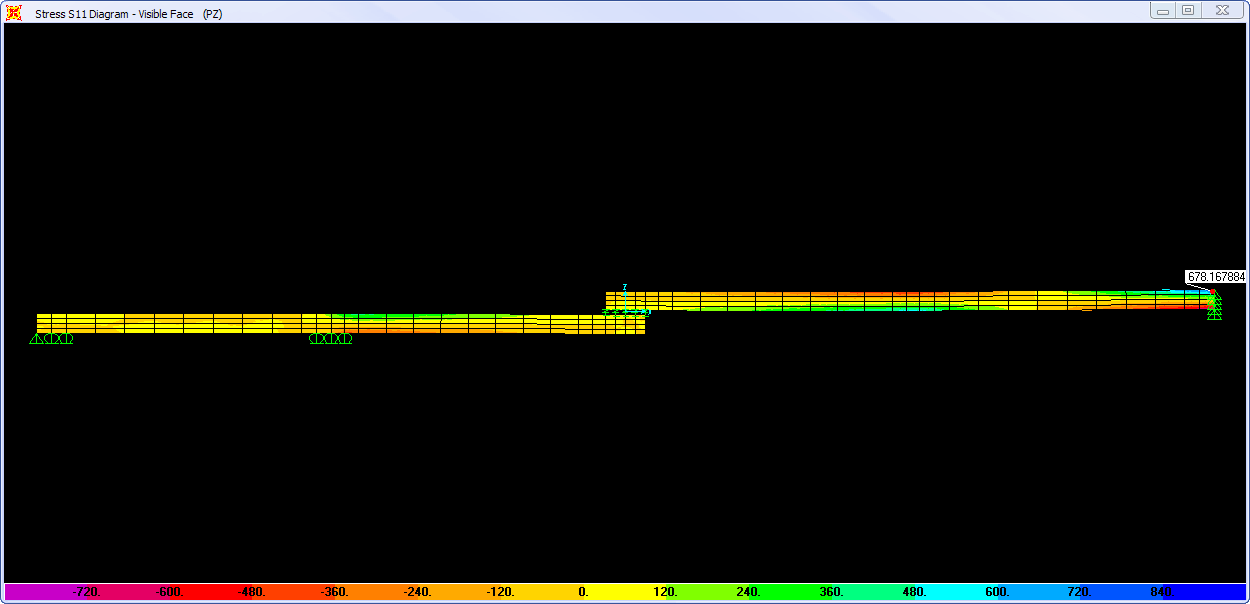
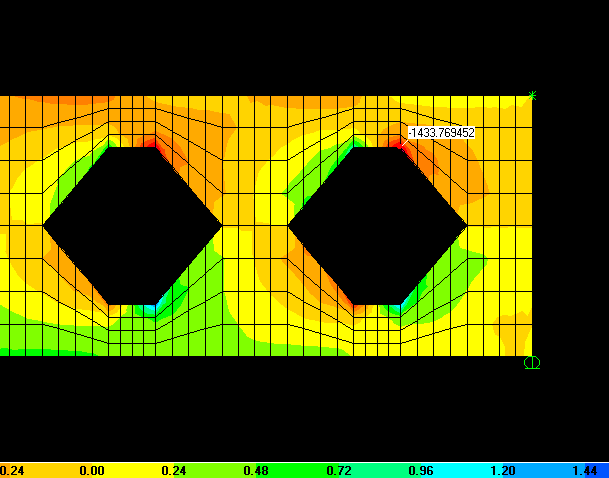
Perbedaan yg cukup signifikan pada hasil analisis asumsi rigid dan elastis adalah distribusi tegangan tanah yg mana pada analisis rigid beban akan diterima merata, sedangkan pada analisis elastis memperhitungkan kekakuan pelat pondasi dan sloof yg menyatu. Akibatnya distribusi moment desain pada derah lapangan dan tumpuan cukup besar perbedaannya, sehingga pembesian yg dipasang lebih besar dari yang dibutuhkan (overdesign/aman) sisi lain tegangan tanah yg terjadi lebih besar terutama pada daerah beban titik kolom, diperkirakan terjadi overstress namun ini masih tercover oleh aksi dua arah serta penentuan angka aman pada nilai tegangan ijin tanah yg biasa diambil nilai sebesar 3 sampai 5, selain itu beban layan yg bekerja yg belum tentu bekerja penuh untuk fungsi kantor beban hidup sebesar 250kg/m^2.

Tambahan:

ada yg comment dan nanya berulang mengenai besarnya nilai CBR thd daya dukung tanah/perkerasan, berikut  sya lampirkan grafiknya (reff. ??? ketinggalan) dari baca2 di google books ttg buku desain perkerasan.

Read More

lateral bracing yg eksentris

penempatan lateral bracing sedapat mungkin garis gaya tepat bertemu dgn center line balok dan kolom, namun karena bebgaia keadaan mungkin perlu bergeser menjadikan tidak tepat dan adanya eksentrisitas.



Ditinjau portal dgn bracing diatas akibat gaya lateral, karena eksentrisitas tsb maka berdasarkan prinsip kesetimbangan (free body diagrams) diperkirakan akan menjadikan momen balok akibat gaya lateral lebih besar dibanding tanpa eksentrisitas seperti yg digambarkan dibawah ini.



Berikut adalah hasil analisa gaya balok akibat beban lateral pada portal dengan bracing yg eksenstris dan tidak.



.



.

.

seperti plot kedua jenis model yg ditinjau tersebut memang pd bracing  dgn eksentrisitas menunjukan momen balok yg lebih besar seperti yg diprediksikan awal. selanjutnya perlu diikutsertakan juga model haunched beam yg nonprismatik agar analisa lebih mendekati.

Read More

dominasi geser pd web balok baja berlubang

Ditinjau distribusi tegangan balok baja berlubang (castellated) WF300 + adding plates dgn tinggi balok jadi 60cm dan bentang 6,1m.



.



.Distribusi tegangan S11 (searah X-global)



. Distribusi tegangan S22 (searah Z-global)



. Lendutan arah-z pd tengah bentang, dz ~ 6.5mm

Dari prediksi perhitungan dibawah menunjukkan bahwa dominasi geser akibat aksi vierendeel sangat berpengaruh terhadap tinjauan desain, keadaan ini juga biasa disebut perilaku lentur lokal. Ditinjau ulang dengan dihilangkannya pelat tambahan, dari kontur tegangan menunjukkan  perbedaan pd kedua jenis balok tsb tidak begitu berpengaruh besar (selisih ~16%), hanya defleksi saja yang terlihat cukup signifikan (selisih ~60%) dikarekan besarnya inersia balok. Mengenai perbedaan distribusi tegangan kedua jenis balok tersebut, agak berbeda dgn prediksi yg seharusnya untuk balok lebih pendek tingginya akan mengalami tegangan lebih besar karena pembagi lengan momen Jd yg lebih kecil. Hal ini perlu peninjauan ulang untuk mencari penyebab perbedaan  tersebut, selain itu perlu juga tinjauan kontribusi geser dari pelat beton komposit.

Dalam step desain bukan ini saja yg menjadikan pertimbangan pemilihan, namun perlu peninjauan lanjut terhadap global buckling (LTB) dan web local buckling hal ini mungkin akan dibahas dikesempatan lain mendatang.



.Distribusi tegangan S11 (searah X-global)



. Lendutan arah-z pd tengah bentang, dz ~ 10.4mm

.

Berikut tabel dan grafik perbedaan hasil perhitungan tangan dan program bantu SAP2000, bertutut-turut adalah model-1 (castellated+adding plates) dan model-2 (castellated only).

.

Terlihat pada titik daerah tumpuan  menunjukan nilai yg lebih besar dari perkiraan sedangkan pada titik lainnya tidak menunjukan itu.



garis kurva warna orange adalah hasil perhitungan tangan, sedangkan garis kurva warna biru tua adalah hasil program SAP2000.



.



.

. ---------- Validation, Calculation pads ------------

.

' beban merata (kgf/cm2)

w = 1.0

' lebar balok flens

b = 15.0

' beban merata (kgf/cm')

q = w*b = 15.00

' bentang balok (cm)

l = 6.106*100 = 610.60

' gaya geser (kgf)

v = 1/2*q*l = 4579.50

' reaksi tumpuan (kgf)

R = v = 4579.50

' tinjauan @ x dari tumpuan (cm)

x = 310.6-289.1 = 21.50

' momen lentur @ x dari tumpuan (kgf.cm)

m = R*x - (1/2 * q * x^2) = 94992.38

Ma = m/100 = 949.92

Va = v - (q*x) = 4257.00

' Check tegangan

tf = 0.8

bf = 14.9

ek = 7.6

' Luas penampang T (cm2)

At = 16.235

' Titik berat ke serat tepi (cm)

x = bs - (((bf * tf) * (tf/2)) + (((bs-tf)*ts)*((bs/2)+tf))/(At)) = 2.41

' Lengan momen (cm)

Jd = 60 - 2*x = 55.17

' Tegangan akibat lentur (kgf/cm2)

Cb = Ma*100/Jd = 1721.79

fb = Cb / At = 106.05

' Tegangan akibat gaya aksial (kgf/cm2)

P = 1.0

fa = P/At = 0.06

' Tegangan akibat gaya lentur & aksial (kgf/cm2)

fn = fb + fa = 106.12

' Tegangan rata-rata (kgf/cm2)

St = 11.17

fs = (Va * 0.5* ek) / St = 1448.22

' Tegangan kombinasi (kgf/cm2)

f = fn + fs = 1554.33

' Tegangan web plate akibat geser (kgf/cm2)

As = 10.6*0.6 = 6.36

P = Va = 4257.00

fsw = P/As = 669.34

' Hasil FE yg dirata-ratakan (kgf/cm2)

fsa = Avg(1566,612,41,534,1505) = 851.60

.

Read More

masalah kontak sederhana suatu balok

masalah kontak sederhana (tanpa gesekan) dapat dianalisa dgn program bantu SAP2000, berikut ditinjau balok kantilever (kanan) yang menerima beban terpusat P. Akibat beban tersebut terjadi defleksi sebesar ~3.5cm, apabila jarak serat tepi bawah balok kanan dgn serat tepi atas balok kiri ada gap lebih kecil dari nilai diatas, maka balok kiri tersebut akan menerima gaya reaksi akibat kontak dari balok kanan.
.
tanpa peninjauan pengaruh kontak

(lendutan -Z)

.

(tegangan lentur S11)

.

tinjauan gap sebesar 0.0 cm

(lendutan -Z)

(tegangan lentur S11)

.
tinjauan gap sebesar 1.0 cm

(lendutan -Z)

(tegangan lentur S11)

.
tinjauan gap sebesar 2.0 cm

(lendutan -Z)

(tegangan lentur S11)

.

Diatas terlihat hasil sesuai dgn yg diprediksikan berdasarkan pendekatan perhitungan dibawah mungkin ini karena bidang kontak yg rata, agak berbeda saat meninjau kontak pane stress model lug/pin bidang kontak lengkung . Terlihat kontur yg tidak menerus pada lingkaran dalam (pin) dgn bidang kontak, perlu peninjaun ulang ini.



.

' Calculation pads
' -------------------
'
' Material props. (kgf,cm)
Es = 2000000
nu = 0.30
G = Es/(2*(1+nu)) = 769230.77
' Section props. (cm)
bs = 5
hs = 10
Is = 1/12*bs*hs^3 = 416.67
Ss = 1/6*bs*hs^2 = 83.33
'
' Cantilever beams (1)
'
' concentrate loads (kgf)
P = 1000
' beam length (cm)
l = 3*100
a = 1.5*100
b = a = 150.00
' Bending moment (kgf.cm)
M = P*b = 150000.00
' Shear force (kgf)
R = P = 1000.00
V = R = 1000.00
' flexural tress (kgf/cm^2)
Sigma = M/Ss = 1800.00
' deflection @ free end (cm)
Delta = ((P*b^2)/(6*Es*Is))*(3*l-b) = 3.37
'
'
' Cantilever beams (2)
'
' concentrate loads (kgf)
P = 1000
' beam length (cm)
l = 3*100
a = 1.5*100
b = a = 150.00
' Bending moment (kgf.cm)
M = 3/16*P*l = 56250.00
' Shear force (kgf)
R1 = 5/16*P = 312.50
R2 = 11/16*P = 687.50
V1 = R1 = 312.50
V2 = R2 = 687.50
' flexural tress (kgf/cm^2)
Sigma = M/Ss = 675.00
' deflection @ point load (cm)
Delta = (7*P*l^3)/(768*Es*Is) = 0.30
'
' overhang beams
'
' concentrate loads (kgf)
P = R1 = 312.50
' beam length (cm)
l = 3*100 = 300.00
a = 1.5*100 = 150.00
x1 = a = 150.00
x = l/2 = 150.00
' Bending moment (kgf.cm)
M1 = P*a = 46875.00
M2 = P*a*x/l = 23437.50
' Shear force (kgf)
R1 = P*a/l = 156.25
R2 = P/l*(l+a) = 468.75
' flexural tress (kgf/cm^2)
Sigma = M1/Ss = 562.50
' deflection @ free end (cm)
Delta = ((P*a^2)/(3*Es*Is))*(l+a) = 1.27

Read More