ikatan antar mesh (FE) yg tidak bertemu #2

tambahan terhadap postingan sya sebelumnya, kali ini menggunakan perintah *SURFACE BEHAVIOR dan PRESSURE-OVERCLOSURE=TIED pada solver FE CalculiX untuk menghubungkan dua buah object yg dimodelkan sebagai elemen shell continuum. diterapkan juga offset pada bagian komponen pelat datar (gray).

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

.

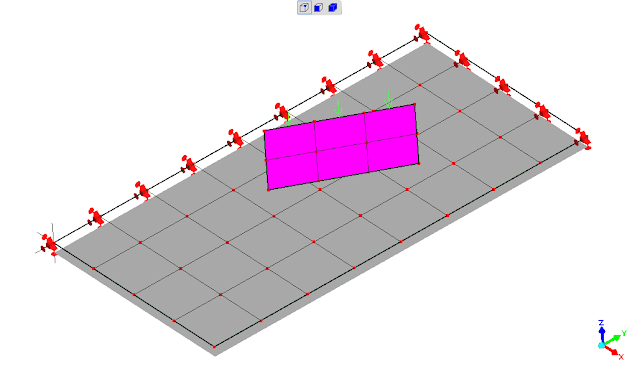
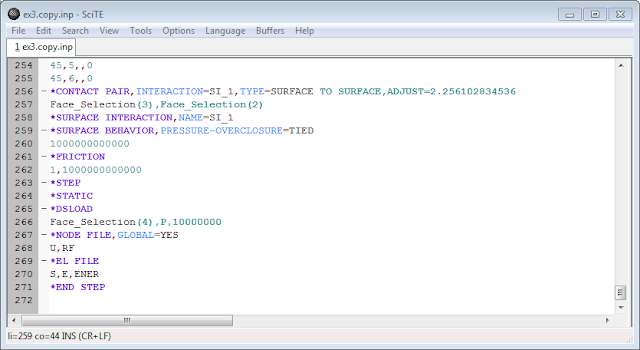
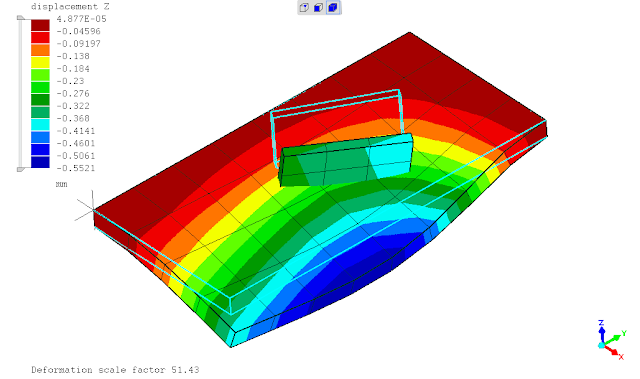
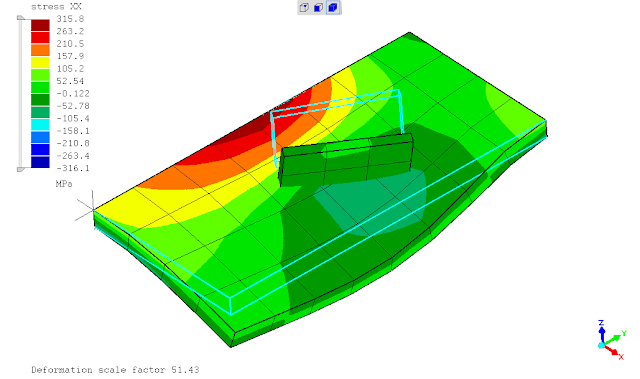
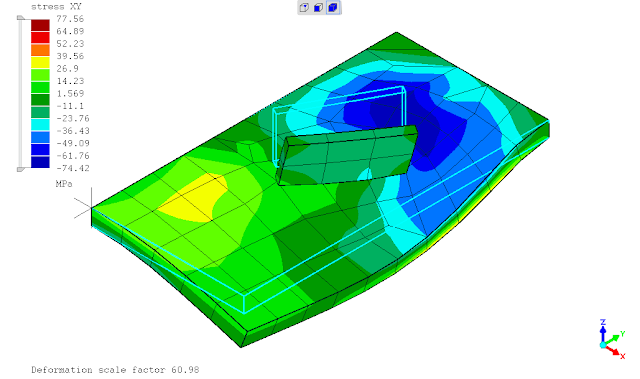
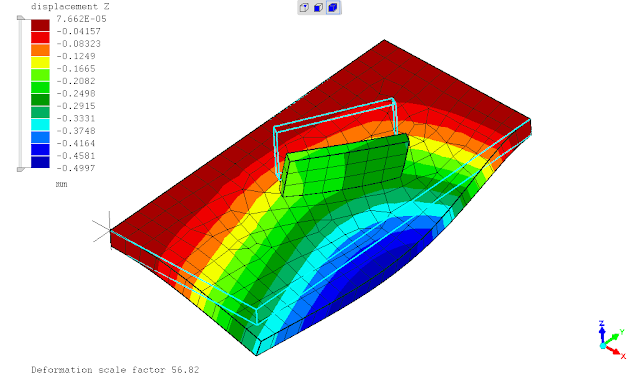
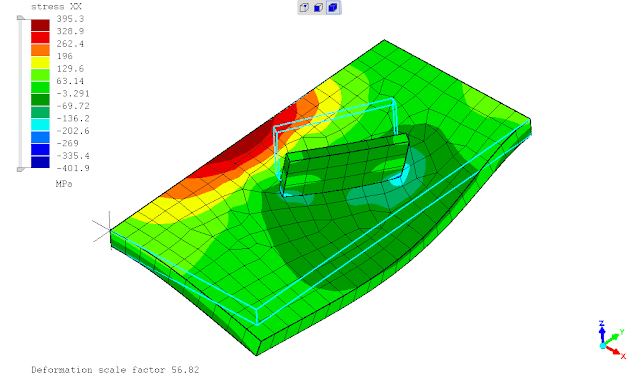
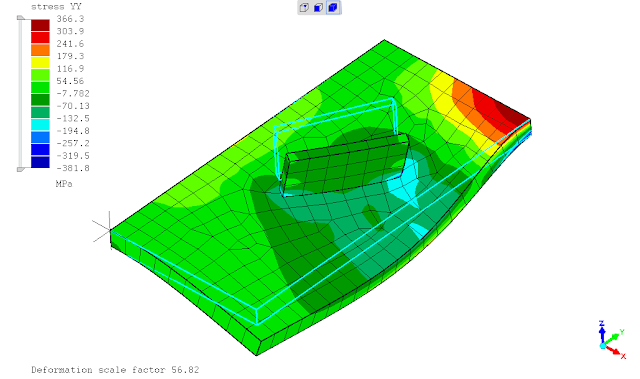
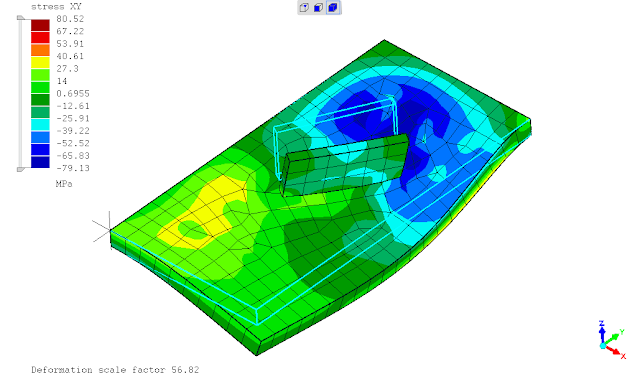
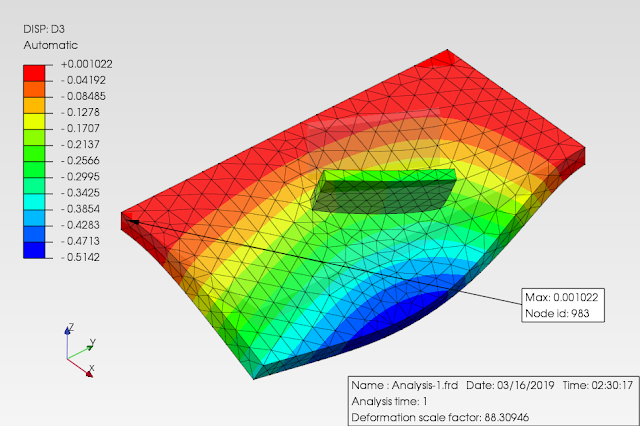
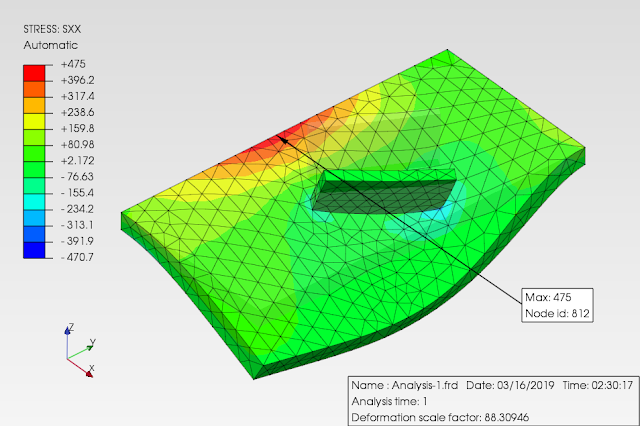
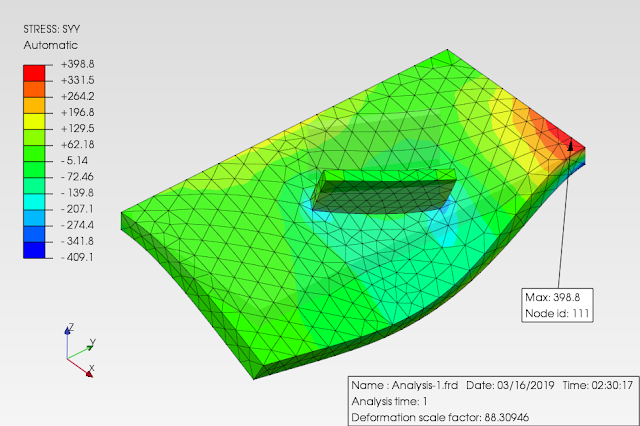
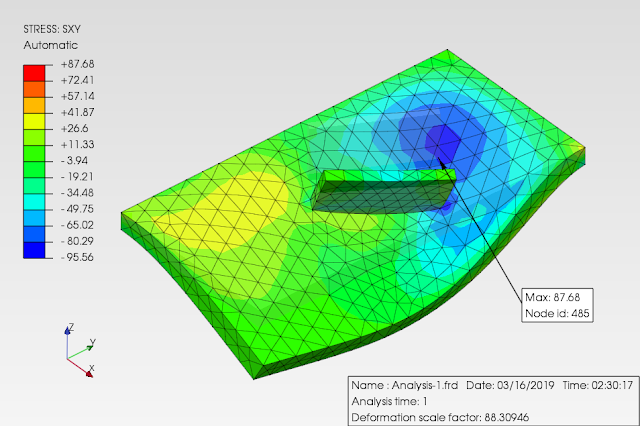
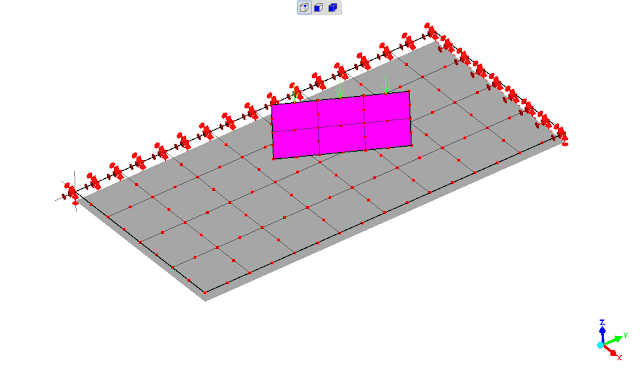
sebagai tambahan perbandingan, berikut hasil menggunakan elemen solid tetahedral quadratic dan mesh yg menerus/menyatu:

.

.

.

.

.

berdasarkan perbandingan hasil dari contoh sederhana diatas, penggunaan hubungan antara komponen pelat tegak & datar dengan penggunaan TIED (mesh discontiuity) maupun cara konvensional dgn mesh menerus hampir cenderung sama, keduanya masih berpengaruh terhadap pias elemen hingga yg digunakan (mesh sensitivity).

.

.

.

.

.

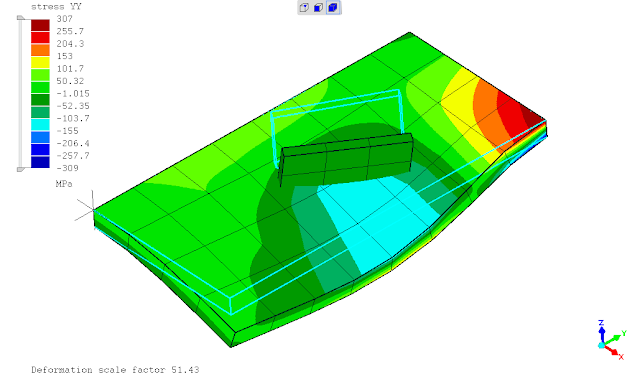
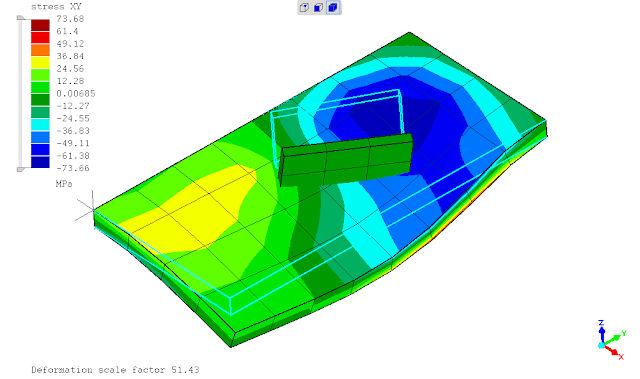
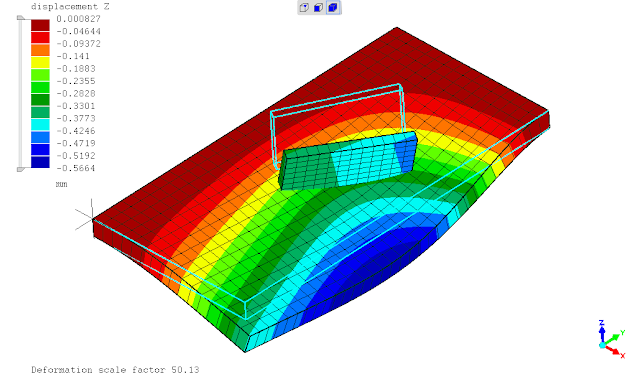
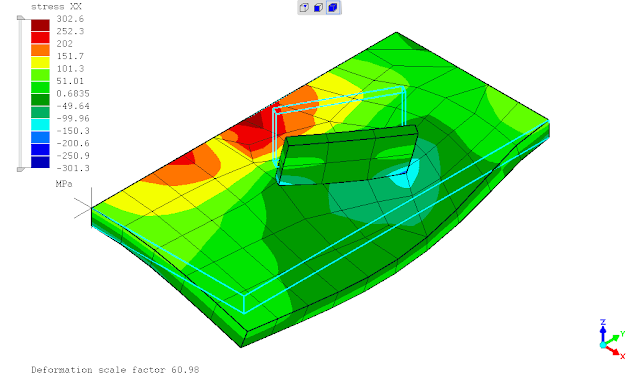
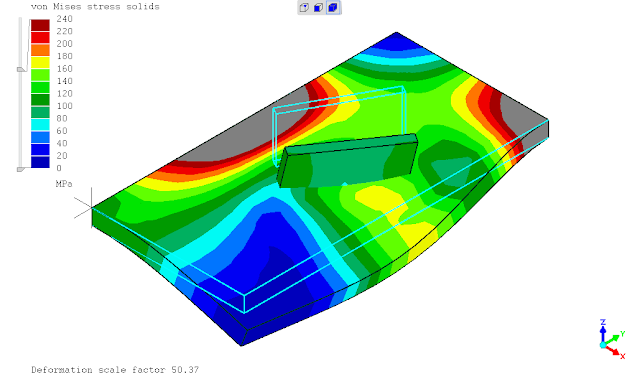
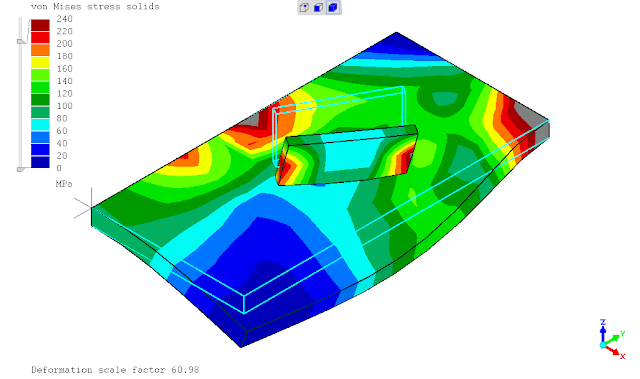
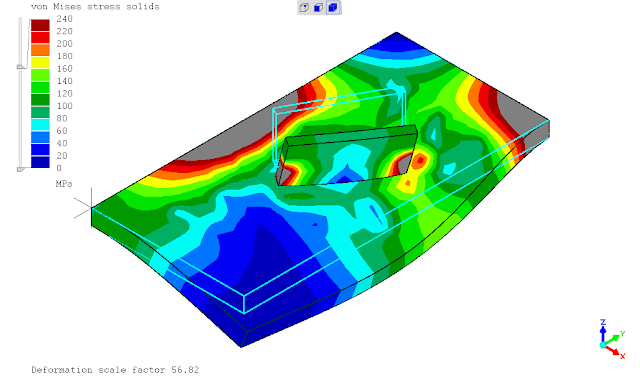
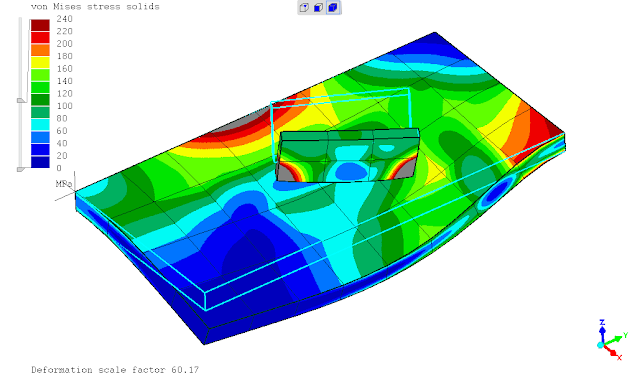
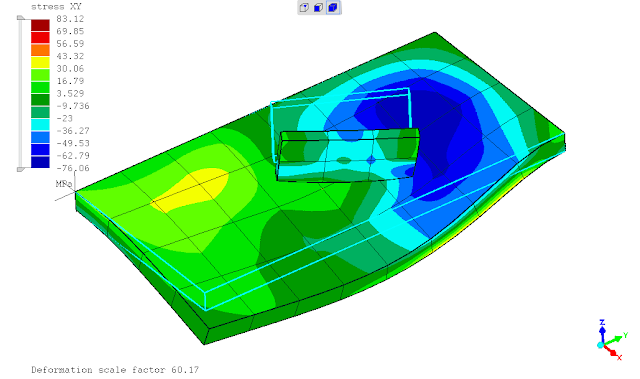
seperti yg telah ditunjukan pada postingan sebelumnya, saat ditinjaun tegangan leleh kriteria Von Mises maka penggunaan *SURFACE BEHAVIOR dan PRESSURE-OVERCLOSURE=TIED tidak dapat mendeteksi titik dimana terjadi maksimum yaitu daerah ujung pertemuan kedua pelat. penghalusan mesh tidak merubah hasil analisa atau keadaan tersebut.

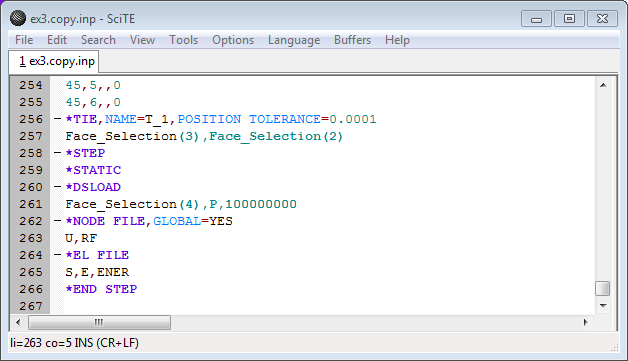
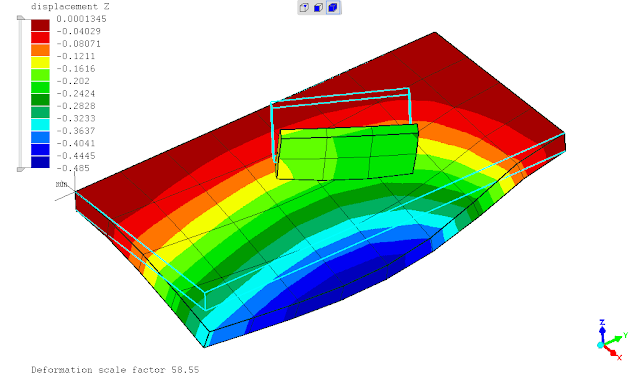
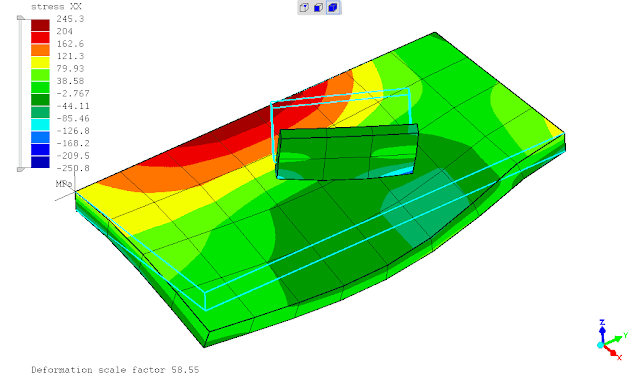
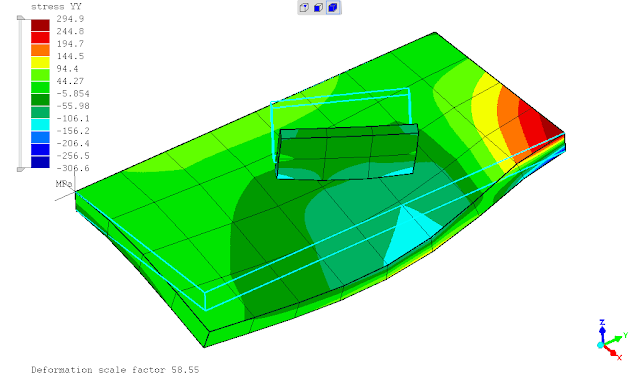
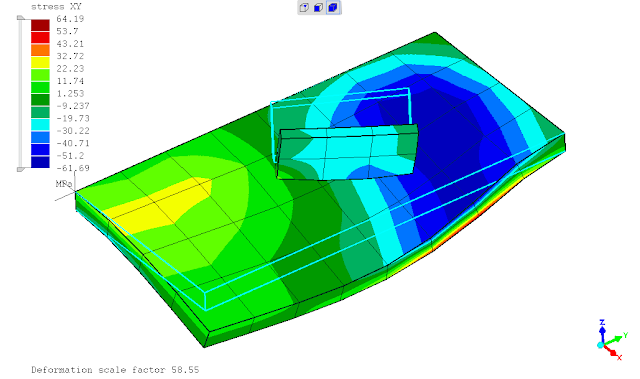
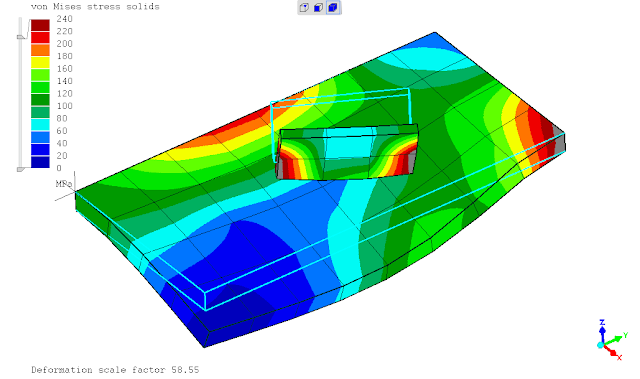
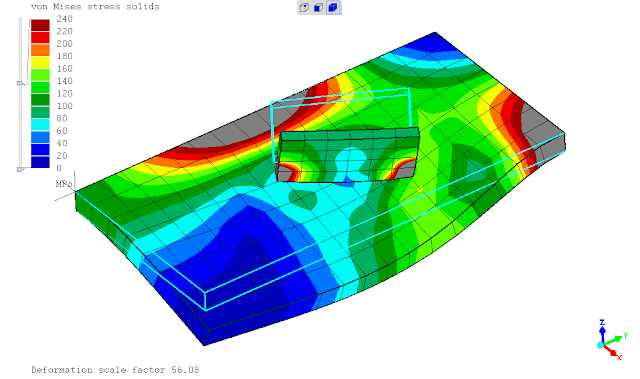
(sumber: Dhondt, 2018)

.

mencoba menggunakan perintah *TIE constraint, terkesan memaksakan karena dalam dokumentasi menunjukkan hal ini tidak diperkenankan namun solver berjalan tanpa kendala dan menampilkan hasil sesuai ekspektasi. keadaan tersebut mungkin dikarenakan ada dokumentasi yg belum updates (?)

.

.

.

.

.

.

.

untuk meningkatkan akurasi hasil digunakan elemen shell continuum jenis quadratic,

.

.

.

.

.

.

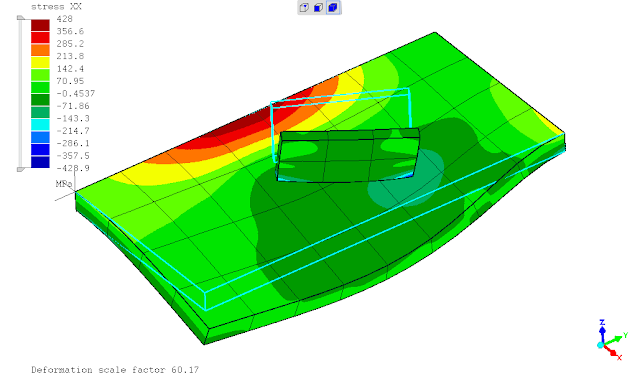
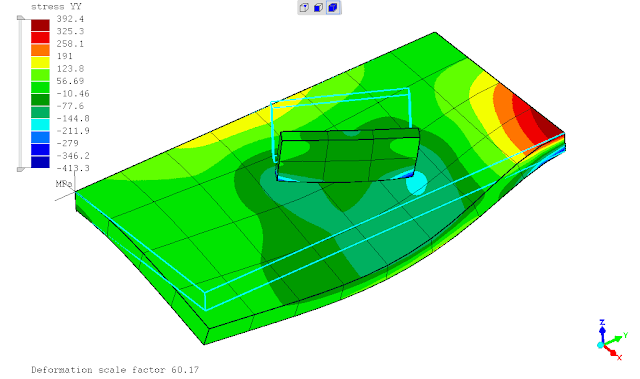
untuk tujuan praktis dalam modeling & solving FE problems direkomendasikan menggunakan elemen SHELL Continuum. terlihat sebelumnya untuk OS 32bit dapat menyelesaikan sampai sekitar 40.000 element atau 600.000 equations selama 100 seconds (Solver Default Cholesky) dan sampai sekitar 55.000 element atau 800.000 equations selama 150 seconds (Solver Iterative Scaling) . perbandingan dgn elemen SOLID yg sampai sekitar 90.000 element atau 400.000 equations selama 130 seconds (Solver Default Cholesky) dan sampai sekitar 300.000 element atau 1.300.000 equations selama 400 seconds (Solver Iterative Scaling)

*FE Software : PPM, MW, SM & CCX