analisa pelat dgn hasil tampilannya tegangan

sebelumnya sya pernah membahas keluaran hasil elemen balok dengan tampilannya tegangan, saat ini yg ditulis adalah untuk elemen pelat. Pada perencanaan beton bertulang yg digunakan adalah hasil keluaran dengan tampilan gaya internal: momen, geser, torsi per unit lebar untuk tujuan perencaanan. Berbeda dengan pelat baja yg membutuhkan tampilan hasil keluaran adalah tegangan dikarenakan material yg homogen dan kriteria tegangan leleh von Mises. Secara prinsip program elemen hinnga untuk elemen pelat klasik menghitung dengan dua cara. keduanya mengacu dari defleksi yg terjadi pada titik pusat elemen berdasarkan asumsi berikut (mengabaikan deformasi geser)

"Points that lie on a line perpendicular to the center plane of the plate remain on a straight line perpendicular to the center plane after deformation."

cara yg pertama yaitu nilai regangan didapat dari hubungan defleksi, sedangkan tegangan diturunkan dari kesetaraan Hooke's law dan kemudian nilai momen dan geser adalah integrasi tegangan pada setebal pelat. Namun cara lain biasanya juga dijelaskan dalam panduan manual software analisa struktur yaitu menggunakan kekakuan lentur pelat (flexural rigidity of plates) dan untuk lebih detailnya merujuk dokumen masing-masing. 

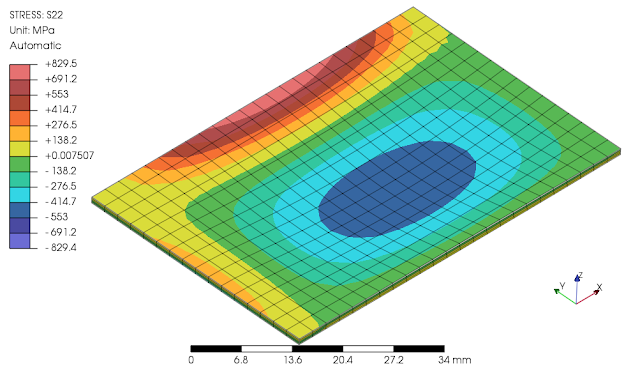
Berikut ditinjau pelat dengan ukuran 40x60mm ketebalan 1.0mm dengan tumpuan sisi jepit dan sederhana. Material yg digunakan adalah baja dengan nilai modulus elastisitas E=200000MPa, beban merata sebesar 1.0N/mm2. Solver elemen hingga yg digunakan adalah OpenSees, OOFEM dan CalculiX.

.

.

.

.

.

.

pada saat export atau konversi dengan NextFEM Designer menjadi format Abaqus, beban merata pada elemen shell dijadikan beban terpusat pada nodes dan ini perlu ditinjau ulang dengan beban merata. Secara internal solver CalculiX melakukan expansi elemen S4 menjadi elemen solid C3D8I. Keluaran bernilai positif adalah tegangan tarik (tension) sedangkan yg bernilai negatif adalah tegangan tekan (compression).

.

.

.

.

.

.

.

.

.

.

.

secara keseluruhan hasil keluaran tegangan dengan solver CalculiX lebih mendekati dengan OOFEM, sedangkan hasil OpenSees menunjukkan lebih besar. Berikut perbandingan lain dengan penggunaan elemen linear solid hexahedral incompatible dan berlapis pada ketebalan pelat serta mesh pembagi yg lebih halus. 

.

.

.

.

.

.

.

berdasarkan perbandingan dengan elemen solid memperlihatkan bahwa formulasi elemen shell linear pada solver OpenSees lebih baik hasilnya jika dibandingkan dengan OOFEM atau CalculiX. Walaupun demikian elemen tersebut cukup sensitif terhadap mesh pembagi sehingga tetap perlu study konvergensi dengan penghalusan (refinement). 

.

.

sebagai tamabahan, CalculiX juga mempunyai elemen shell dengan formulasi klasik atau konvensional namun sdh ada perbaikan updates. Hasilnya menunjukkan lebih baik dibanding jenis S4 expanded di CalculiX, dan juga jenis S4 konvensional OpenSees atau OOFEM berdasarkan konsep Mixed Interpolation of Tensorial Components (MITC4).

"A new three-node shell element with six degrees of freedom per node—three translations and three rotations—is presented in this paper. The discrete shear gap approach together with the cell smoothing technique is implemented for treatment of shear locking. The membrane behavior is resolved by means of the assumed natural deviatoric strains formulation with certain adjustments implemented to accommodate for shell behavior. (Gil Rama etal, 2018)"

.

.

.

.

.

.

.

.

dan juga perbandingannya dengan hasil keluaran dari SAP2000 Student Version 7.40, terlihat hanya terpaut selisih sedikit dan menunjukan lebih akurat.

,

.

.

.

.